题目内容
4.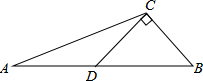 如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.
如图,CD是△ABC的中线,CD⊥CB,∠ACD=30°,求证:AC=2BC.
分析 延长CD至E,使DE=DC,连接BE;由SAS证明△BDE≌△ADC,得出BE=AC,∠E=∠ACD=30°,由含30°角的直角三角形的性质得出BE=2BC,即可得出AC=2BC.
解答 证明:延长CD至E,使DE=DC,连接BE,如图所示:
∵CD是△ABC的中线,
∴BD=AD,
在△BDE和△ADC中,
$\left\{\begin{array}{l}{BD=AD}&{\;}\\{∠BDE=∠ADC}&{\;}\\{DE=DC}&{\;}\end{array}\right.$,
∴△BDE≌△ADC(SAS),
∴BE=AC,∠E=∠ACD=30°,
∵CD⊥CB,
∴∠BCE=90°,
∴BE=2BC,
∴AC=2BC.
点评 本题考查了全等三角形的判定与性质、含30°角的直角三角形的性质;通过作辅助线构造三角形全等是解决问题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
11.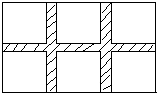 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )| A. | 100×80-100x-80×2x=7488 | B. | (100-2x)(80-x)=7488 | ||
| C. | (100-2x)(80-x)+2x2=7488 | D. | 100x+80×2x=512 |
 如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证:
如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证: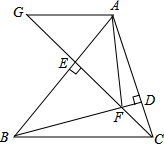 如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45°
如图.在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE交于点F,∠BCE=45°  如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.
如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.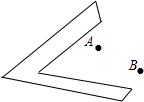 如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.
如图,在两相交公路有两村庄A、B,要修一个商店,要求到两村庄A、B的距离相等.到两公路的距离也相等.请你利用几何作图的方法,在下面的示意图中画出商店的位置.