题目内容
19.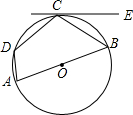 如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )
如图,已知四边形ABCD内接于⊙O,AB是⊙O的直径,EC与⊙O相切于点C,∠ECB=35°,则∠D的度数是( )| A. | 145° | B. | 125° | C. | 90° | D. | 80° |
分析 连接BD,由AB是⊙O的直径,得∠ADB=90°,再由EC与⊙O相切于点C,∠ECB=35°,知∠BDC=35°,从而得出∠D的度数.
解答  解:连接BD,
解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵EC与⊙O相切,∠ECB=35°,
∴∠BDC=35°,
∴∠D=∠ADB+∠BDC=90°+35°=125°,
故选B.
点评 本题考查了切线的性质,以及弦切角定理和应用,解题时要认真审题,仔细解答,合理进行等价转化.

练习册系列答案
相关题目
7.下列说法错误的是( )
| A. | π是有理数 | B. | 两点之间线段最短 | ||
| C. | x2-x是二次二项式 | D. | 正数的绝对值是它本身 |
11.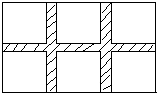 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
 如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )
如图,公园要在一块长为100米,宽为80米的矩形场地上修建三条宽度相等的道路,其中两条纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为x米,则可列方程为( )| A. | 100×80-100x-80×2x=7488 | B. | (100-2x)(80-x)=7488 | ||
| C. | (100-2x)(80-x)+2x2=7488 | D. | 100x+80×2x=512 |
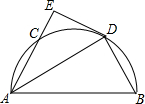 如图所示,AB为半圆O的直径,C是半圆上一点,AD平分∠CAB交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E.
如图所示,AB为半圆O的直径,C是半圆上一点,AD平分∠CAB交半圆于点D,过点D作DE⊥AC,DE交AC的延长线于点E. 如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证:
如图,正三角形ABC中,在AB,AC边上分别取点M,N使BM=AN,连BN,CM,求证: