题目内容
15. 如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE
如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE(1)求AG的长;
(2)请你添加一个条件,使四边形AGCH是平行四边形,并简单说明理由.
分析 (1)首先证明四边形ADEF是平行四边形,再证明四边形ABCD是平行四边形,可得AB=DC=6,AB∥CD,再证明BC=BG,可得BG的长度,进而可得答案;
(2)添加AF∥CG,根据两组对边分别平行的四边形是平行四边形进行判定即可.
解答  解:(1)∵AF∥DE,AF=DE,
解:(1)∵AF∥DE,AF=DE,
∴四边形ADEF是平行四边形,
∴AD∥BE,AD=EF,
∴AD∥CB,
∵BC=EF,
∴AD=BC,
∴四边形ABCD是平行四边形,
∴AB=DC=6,AB∥CD,
∴∠3=∠2,
∵CG平分∠BCD,
∴∠1=∠2,
∴∠3=∠1,
∴BC=BG=4,
∴AG=6-4=2;
(2)添加GC∥AF,
理由:∵AF∥GC,AB∥DC,
∴四边形AGCH是平行四边形.
点评 此题主要考查了平行四边形的判定和性质,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
7.三条边都是质数的三角形可能是( )
①锐角三角形②直角三角形③钝角三角形④等腰三角形⑤等边三角形.
①锐角三角形②直角三角形③钝角三角形④等腰三角形⑤等边三角形.
| A. | ①②③④ | B. | ②③④⑤ | C. | ①③④⑤ | D. | ①②③④⑤ |
4.等腰锐角三角形ABC中,AB=AC,若它腰上的高等于腰长的一半,则这个等腰三角形的底角等于( )
| A. | 15° | B. | 30° | C. | 60° | D. | 75° |
 如图,分别过△ABC的顶点作它的对边的平行线围成△A′B′C′,则共有3个平行四边形;若△ABC的周长为1,则△A′B′C′的周长为2.
如图,分别过△ABC的顶点作它的对边的平行线围成△A′B′C′,则共有3个平行四边形;若△ABC的周长为1,则△A′B′C′的周长为2. 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是18$\sqrt{3}$-9π.
如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是18$\sqrt{3}$-9π. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=3,则△OCE的面积为( )
如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=3,则△OCE的面积为( )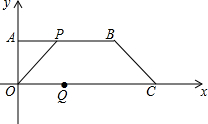 在平面直角坐标系中,有点A(0,4)、B(9,4),C(12,0).已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动.运动速度都是每秒一个单位长度,运动时间为t秒.
在平面直角坐标系中,有点A(0,4)、B(9,4),C(12,0).已知点P从点A出发沿AB路线向点B运动,点Q从点C出发沿CO路线向点O运动.运动速度都是每秒一个单位长度,运动时间为t秒. 如图,某同学利用学校某建筑物测量旗杆的高度,他在C点处测得旗杆顶部A点的仰角为31°,旗杆底部B点的俯角为44°.若旗杆底部B点到该建筑的水平距离BE=6米,旗杆台阶高1米,求旗杆顶部A离地面的高度.(结果保留整数,参考数据:sin44°$≈\frac{7}{10}$,cos44°$≈\frac{7}{10}$,tan44°≈1,sin31°$≈\frac{1}{2}$,cos31°$≈\frac{9}{10}$,tan31°$≈\frac{3}{5}$)
如图,某同学利用学校某建筑物测量旗杆的高度,他在C点处测得旗杆顶部A点的仰角为31°,旗杆底部B点的俯角为44°.若旗杆底部B点到该建筑的水平距离BE=6米,旗杆台阶高1米,求旗杆顶部A离地面的高度.(结果保留整数,参考数据:sin44°$≈\frac{7}{10}$,cos44°$≈\frac{7}{10}$,tan44°≈1,sin31°$≈\frac{1}{2}$,cos31°$≈\frac{9}{10}$,tan31°$≈\frac{3}{5}$)