题目内容
3. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=3,则△OCE的面积为( )
如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数$y=\frac{4}{x}$的图象经过点C,且与AB交于点E.若OD=3,则△OCE的面积为( )| A. | 2 | B. | 5 | C. | 12 | D. | 10 |
分析 连接AC,由条件可求得CD的长,可求得△OAC的面积,再结合菱形的性质可知S△OCE=S△OAC,可求得答案.
解答 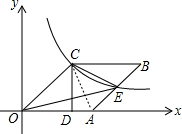 解:
解:
如图,连接AC,
∵OD=3,CD⊥x轴,
∴OD×CD=xy=4,
解得CD=$\frac{4}{3}$,由勾股定理,得OC=$\sqrt{O{D}^{2}+C{D}^{2}}$=$\frac{5}{3}$,
由菱形的性质,可知OA=OC,
∵△OCE与△OAC同底等高,
∴S△OCE=S△OAC=$\frac{1}{2}$×OA×CD=$\frac{1}{2}$×$\frac{5}{3}$×3=10.
故选D.
点评 本题主要考查反比例函数图象上点的坐标特征及菱形的性质,根据菱形的性质得到S△OCE=S△OAC是解题的关键.

练习册系列答案
相关题目
11. 如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
 如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.
如图,∠ACB=90°,CD⊥AB,垂足为D,则点A到CD的距离可用线段( )的长度来表示.| A. | AC | B. | AD | C. | AB | D. | CD |
 是
是  的弦,
的弦,  是
是  的切线,
的切线,  为切点,
为切点,  经过圆心,若
经过圆心,若  ,则
,则  的大小等于( )
的大小等于( ) 
 B.
B. 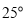 C.
C.  D.
D. 
 如图,正方形ABCD的边长为1cm,AC是对角线,AE平分∠BAC,EF⊥AC于F.
如图,正方形ABCD的边长为1cm,AC是对角线,AE平分∠BAC,EF⊥AC于F. 如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE
如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE 如图所示,四边形ABCD为平行四边形,在AB、AD边上各作正方形ABEF,ADGH,求证:平行四边形对角线AC与FH垂直.
如图所示,四边形ABCD为平行四边形,在AB、AD边上各作正方形ABEF,ADGH,求证:平行四边形对角线AC与FH垂直.