Question

10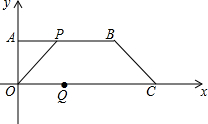．在平面直角坐标系中，有点A（0，4）、B（9，4），C（12，0）．已知点P从点A出发沿AB路线向点B运动，点Q从点C出发沿CO路线向点O运动．运动速度都是每秒一个单位长度，运动时间为t秒．
（1）当四边形AQCB是平行四边形时，求t值．
（2）连接PQ，当四边形APQO是矩形时，求t值．

Answer 1

分析 （1）用含t的代数式表示出来CQ，根据平行四边形的性质即可得出AB=CQ，从而得出关于时间t的一元一次方程，解方程即可得出结论；
（2）用含t的代数式表示出来AP和OQ，根据矩形的性质即可得出AP=OQ，从而得出关于时间t的一元一次方程，解方程即可得出结论．

解答 解：（1）当四边形AQCB是平行四边形时，有AB=CQ，
∵A（0，4）、B（9，4），C（12，0），
∴AB=9，OC=12，AB∥OC．
∵CQ=t，
∴t=9．
∴当四边形AQCB是平行四边形时，t的值为9秒．
（2）当四边形APQO是矩形时，有AP=OQ，
∵AP=t，OQ=OC-CQ=12-t，
∴t=12-t，
解得：t=6．
∴当四边形APQO是矩形时，t的值为6秒．

点评 本题考查了矩形的性质、坐标与图形的性质以及平行四边形的性质，解题的关键是：（1）找出关于时间t的一元一次方程；（2）找出关于时间t的一元一次方程．本题属于中档题，难度不大，解决该题型题目时，熟记平行四边形与矩形的性质是关键．