题目内容
5. 如图,分别过△ABC的顶点作它的对边的平行线围成△A′B′C′,则共有3个平行四边形;若△ABC的周长为1,则△A′B′C′的周长为2.
如图,分别过△ABC的顶点作它的对边的平行线围成△A′B′C′,则共有3个平行四边形;若△ABC的周长为1,则△A′B′C′的周长为2.
分析 根据两组对边分别平行的四边形是平行四边形可得四边形BCB′A是平行四边形,四边形A′CAB是平行四边形,四边形CAC′B是平行四边形;根据平行四边形对边分别相等可得CB=A′B′,AB=B′C,A′C=AB,AC=A′B=C′B,CB=AC′,进而可得△A′B′C′的周长是△ABC的周长的2倍,进而可得答案.
解答 解:∵A′B′∥AB,CB∥B′C′,
∴四边形BCB′A是平行四边形,
同理:四边形A′CAB是平行四边形,四边形CAC′B是平行四边形,
平行四边形共3个;
∵四边形BCB′A是平行四边形,
∴CB=A′B′,AB=B′C,
同理:A′C=AB,AC=A′B=C′B,CB=AC′,
∵△ABC的周长为1,
∴△A′B′C′的周长为2,
故答案为:3;2.
点评 此题主要考查了平行四边形的判定和性质,关键是掌握两组对边分别平行的四边形是平行四边形,平行四边形对边分别相等.

练习册系列答案
相关题目
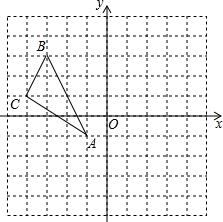 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1) 交
交  轴于点
轴于点  和点
和点  ,交
,交  轴于点
轴于点  .
.  在抛物线上,且
在抛物线上,且  ,求点
,求点  的坐标;
的坐标; 是线段
是线段  上的一动点,作
上的一动点,作  轴,交抛物线于点
轴,交抛物线于点  ,求线段
,求线段  长度的最大值.
长度的最大值.
 是
是  的弦,
的弦,  是
是  的切线,
的切线,  为切点,
为切点,  经过圆心,若
经过圆心,若  ,则
,则  的大小等于( )
的大小等于( ) 
 B.
B. 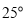 C.
C.  D.
D. 
 ,
,  ,
,  ,
,  ,其中最小的是( )
,其中最小的是( ) B.
B.  C.
C.  D.
D. 
 平行四边形各内角平分线所围成的四边形是什么图形?请证明你的观点.
平行四边形各内角平分线所围成的四边形是什么图形?请证明你的观点. 如图是李峰家一块平行四边形花圃,周长为36cm,且DE⊥AB,DF⊥BC,DE=5,DF=7,求花圃的面积.
如图是李峰家一块平行四边形花圃,周长为36cm,且DE⊥AB,DF⊥BC,DE=5,DF=7,求花圃的面积. 如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE
如图,点B,C,F在同一直线上,AF∥DE,CG平分∠BCD,CD=6,BC=EF=4,AF=DE