题目内容
3.已知,|a|=-a,$\frac{|b|}{b}$=-1,|c|=c,化简|a+b|-|a-c|-|b-c|=-2c.分析 根据题意,利用绝对值的代数意义判断出a,b,c的正负,原式利用绝对值的代数意义化简即可得到结果.
解答 解:∵|a|=-a,$\frac{|b|}{b}$=-1,|c|=c,
∴a为非正数,b为非正数,c为非负数,
∴a+b≤0,a-c≤0,b-c≤0,
则原式=-a-b+a-c+b-c=-2c,
故答案为:-2c
点评 此题考查了有理数的减法,以及绝对值,熟练掌握绝对值的代数意义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.将抛物线y=-x2向左移动2个单位,再向上移动3个单位后,抛物线的顶点为( )
| A. | (2,3) | B. | (2,-3) | C. | (-2,3) | D. | (-2,-3) |
11. 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
 如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.
如图,甲、乙、丙、丁四个扇形的面积之比是1:2:3:4,则甲、乙、丙、丁四个扇形中圆心角度数最大的是( )度.| A. | 36 | B. | 72 | C. | 144 | D. | 156 |
16.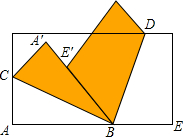 如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
 如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )
如图,将一张长方形纸片的角A、E分别沿着BC、BD折叠,点A落在A'处,点E落在边BA'上的E'处,则∠CBD的度数是( )| A. | 85° | B. | 90° | C. | 95° | D. | 100° |
 已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2. 如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长.
如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长.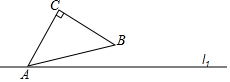 点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹.
点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹. 如图,已知函数y=-2x+4的图象,观察图象回答下列问题:
如图,已知函数y=-2x+4的图象,观察图象回答下列问题: