题目内容
13. 已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
已知Rt△DEF按如图所示的位置放置,∠E=90°,∠EDF=30°,DE=6$\sqrt{3}$,点H为线段FD延长线上一动点,现将△DEH绕点D顺时针旋转60°得到△DAK,E的对应点是A,H的对应点是K,若△EHK的面积为4$\sqrt{3}$,则DH的值为2.
分析 将△DEH绕点D顺时针旋转60°得到△DAK,得到△KDH是等边三角形,求得∠EDK=180°-∠EDF-∠KDH=90°,作HG⊥ED于G,设DH=x,根据直角三角形的性质得到HG=$\frac{1}{2}$x,根据三角形的面积列方程即可得到结论.
解答  解:∵将△DEH绕点D顺时针旋转60°得到△DAK,
解:∵将△DEH绕点D顺时针旋转60°得到△DAK,
∴△KDH是等边三角形,
∵∠EDK=180°-∠EDF-∠KDH=90°,
作HG⊥ED于G,
∴∠HDG=30°,
设DH=x,
∴HG=$\frac{1}{2}$x,
∵S△EDH=$\frac{1}{2}$DE•HG=$\frac{1}{2}$DE•$\frac{1}{2}$x=$\frac{1}{4}$DE•x,S△EDK=$\frac{1}{2}$DE•DK=$\frac{1}{2}$DE•x,S△DKH=$\frac{1}{2}$•$\frac{\sqrt{3}}{2}$x2=$\frac{\sqrt{3}}{4}$x2,
∴S△EKH=S△EDK+S△DKH+D△EDH=$\frac{1}{2}$DE•x++$\frac{\sqrt{3}}{4}$x2-$\frac{1}{4}$DE•x=3$\sqrt{3}$x+$\frac{\sqrt{3}}{4}$x2-$\frac{3\sqrt{3}}{2}$x=4$\sqrt{3}$,
∴x=2,
∴DH=x=2.
故答案为:2.
点评 本题考查了旋转的性质,含30°角的直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )
 某几何体的主视图和左视图如图所示,则该几何体可能是( )
某几何体的主视图和左视图如图所示,则该几何体可能是( )| A. | 长方体 | B. | 圆锥 | C. | 正方体 | D. | 球 |
5. 如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
 如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )
如图是正方体的一个展开图,相对面上的数字或代数式相等,则x+2y-3z=( )| A. | -4 | B. | 6 | C. | 8 | D. | 12 |
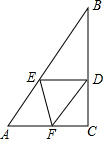 如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
如图,Rt△ABC中,∠C=90°,∠B=30°,点D在BC上,BD=2CD,过D点作BC的垂线交AB于点E,BE=6cm,F为线段AC上一动点,则△DEF的周长最小值为9cm.
