题目内容
14.不等式组$\left\{\begin{array}{l}{x+5<5x+1}\\{x-m>1}\end{array}\right.$的解集是x>1,则m的取值范围是( )| A. | m≥1 | B. | m≤1 | C. | m≥0 | D. | m≤0 |
分析 表示出不等式组中两不等式的解集,根据已知不等式组的解集确定出m的范围即可.
解答 解:不等式整理得:$\left\{\begin{array}{l}{x>1}\\{x>m+1}\end{array}\right.$,
由不等式组的解集为x>1,得到m+1≤1,
解得:m≤0,
故选D
点评 此题考查了不等式的解集,熟练掌握不等式组取解集的方法是解本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
9.已知二次函数y=ax2-bx-2(a≠0)的图象的顶点在第四象限,且过点(-1,0),当a-b为整数时,ab的值为( )
| A. | $\frac{3}{4}$或1 | B. | $\frac{1}{4}$或1 | C. | $\frac{3}{4}$或$\frac{1}{2}$ | D. | $\frac{1}{4}$或$\frac{3}{4}$ |
6. 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
 如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
如图,在网格中(每个小正方形的边长均为1个单位)选取9个格点(格线的交点称为格点).如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )| A. | 2$\sqrt{2}$<r≤$\sqrt{17}$ | B. | $\sqrt{17}$<r≤3$\sqrt{2}$ | C. | $\sqrt{17}$<r≤5 | D. | 5<r≤$\sqrt{29}$ |
3.函数y=$\sqrt{2x-4}$中自变量x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≤2 | D. | x≠2 |
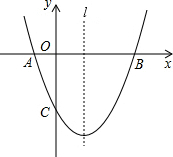 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.