题目内容
9.已知二次函数y=ax2-bx-2(a≠0)的图象的顶点在第四象限,且过点(-1,0),当a-b为整数时,ab的值为( )| A. | $\frac{3}{4}$或1 | B. | $\frac{1}{4}$或1 | C. | $\frac{3}{4}$或$\frac{1}{2}$ | D. | $\frac{1}{4}$或$\frac{3}{4}$ |
分析 首先根据题意确定a、b的符号,然后进一步确定a的取值范围,根据a-b为整数确定a、b的值,从而确定答案.
解答 解:依题意知a>0,-$\frac{-b}{2a}$>0,a+b-2=0,
故b>0,且b=2-a,a-b=a-(2-a)=2a-2,
于是0<a<2,
∴-2<2a-2<2,
又∵a-b为整数,
∴2a-2=-1,0,1,
故a=$\frac{1}{2}$,1,$\frac{3}{2}$,
b=$\frac{3}{2}$,1,$\frac{1}{2}$,
∴ab=$\frac{3}{4}$或1.
故选A.
点评 本题考查了二次函数的性质,解题的关键是能够根据图象经过的点确定a+b+c的值和a、b的符号,难度中等.

练习册系列答案
相关题目
20.某商场利用摸奖开展促销活动,中奖率为$\frac{1}{3}$,则下列说法正确的是( )
| A. | 若摸奖三次,则至少中奖一次 | |
| B. | 若连续摸奖两次,则不会都中奖 | |
| C. | 若只摸奖一次,则也有可能中奖 | |
| D. | 若连续摸奖两次都不中奖,则第三次一定中奖 |
4.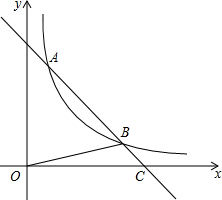 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
 如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )
如图,直线y=-x+5与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.若将直线y=-x+5向下平移1个单位,则所得直线与双曲线y=$\frac{k}{x}$(x>0)的交点有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个,或1个,或2个 |
14.不等式组$\left\{\begin{array}{l}{x+5<5x+1}\\{x-m>1}\end{array}\right.$的解集是x>1,则m的取值范围是( )
| A. | m≥1 | B. | m≤1 | C. | m≥0 | D. | m≤0 |
18.下列运算正确的是( )
| A. | (-2a3)2=-4a6 | B. | $\sqrt{9}$=±3 | C. | m2•m3=m6 | D. | x3+2x3=3x3 |
19.月球的直径约为3476000米,将3476000用科学记数法表示应为( )
| A. | 0.3476×102 | B. | 34.76×104 | C. | 3.476×106 | D. | 3.476×108 |
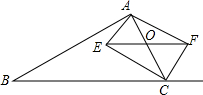 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.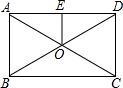 如图,已知:矩形ABCD中对角线,AC,BD交于点O,E是AD中点,连接OE.若OE=3,AD=8,则对角线AC的长为( )
如图,已知:矩形ABCD中对角线,AC,BD交于点O,E是AD中点,连接OE.若OE=3,AD=8,则对角线AC的长为( )