题目内容
4.为了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等5项体育活动的喜欢程度,某校随机抽查部分学生,对他们最喜欢的体育项目(每人只选一项)进行了问卷调查,并将统计数据绘制成如下两幅不完整的统计图:请解答下列问题:
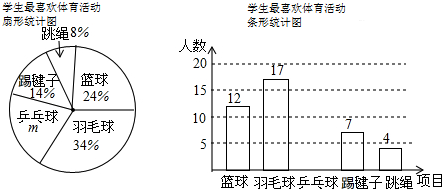
(1)m=20%,这次共抽取了50名学生进行调查;请补全条形统计图;
(2)若全校有800名学生,则该校约有多少名学生喜爱打篮球?
(3)学校准备从喜欢跳绳活动的4人(二男二女)中随机选取2人进行体能测试,求抽到一男一女学生的概率是多少?
分析 (1)由扇形统计图的知识,可求得m的值,继而求得抽取了的学生数,则可补全条形统计图;
(2)利用样本估计总体的方法,即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与抽到一男一女学生的情况,再利用概率公式即可求得答案.
解答 解:(1)∵m%=1-14%-8%-24%-34%=20%,
∴m=20,
∵喜欢跳绳的占8%,有4人,
∴4÷8%=50(名),
∴共抽取了50名学生;
故答案为:20,50;
喜欢乒乓球的:50×20%=10(名),
条形统计图如图所示;
(2)∵800×24%=192,
∴该校约有192名学生喜爱打篮球;
(3)画树状图得:
∵可能的情况一共有12种,抽到“一男一女”学生的情况有8种,
∴抽到“一男一女”学生的概率是:$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查了列表法或树状图法求概率以及扇形与条形统计图.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
5.某个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
15.已知等腰三角形的一边长为3cm,且它的周长为12cm,则它的底边长为( )
| A. | 3cm | B. | 6cm | C. | 9cm | D. | 3cm或6cm |
12.计算:1-1×(-3)=( )
| A. | 0 | B. | 4 | C. | -4 | D. | 5 |
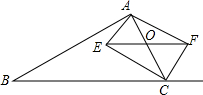 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F.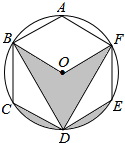 如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π.
如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π.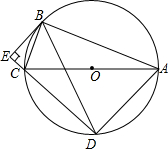 如图,⊙O是△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.