题目内容
19.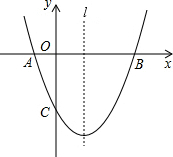 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
分析 (1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
解答 解:(1)将A(-1,0)、B(3,0)、C(0,-3)代入抛物线y=ax2+bx+c中,得:
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$
故抛物线的解析式:y=x2-2x-3.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,
此时x=-$\frac{b}{2a}$=1,
故P(1,0);
(3)如图所示:抛物线的对称轴为:x=-$\frac{b}{2a}$=1,设M(1,m),已知A(-1,0)、C(0,-3),则:
MA2=m2+4,MC2=(3+m)2+1=m2+6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:
m2+4=m2+6m+10,解得:m=-1,
②若MA=AC,则MA2=AC2,得:
m2+4=10,得:m=±$\sqrt{6}$;
③若MC=AC,则MC2=AC2,得:
m2+6m+10=10,得:m1=0,m2=-6;
当m=-6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,$\sqrt{6}$)(1,-$\sqrt{6}$)(1,-1)(1,0).
点评 此题主要考查了二次函数综合题涉及了抛物线的性质及解析式的确定、等腰三角形的判定等知识,在判定等腰三角形时,一定要根据不同的腰和底分类进行讨论,以免漏解.

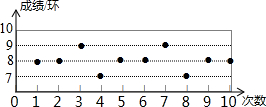 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.| 甲 | 乙 | 丙 | |
| 平均数 | 7.9 | 7.9 | 8.0 |
| 方差 | 3.29 | 0.49 | 1.8 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
| A. | m≥1 | B. | m≤1 | C. | m≥0 | D. | m≤0 |
| A. | 0.995×105 | B. | 9.95×105 | C. | 9.95×104 | D. | 9.5×104 |
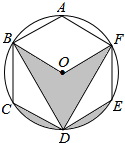 如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π.
如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π. 如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2$\sqrt{6}$.
如图,正方形ABCD内接于⊙O,其边长为4,则⊙O的内接正三角形EFG的边长为2$\sqrt{6}$.