题目内容
9.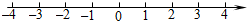 完成下列各题:
完成下列各题:(1)化简:(1+x)(1-x)+x(x+2)-1
(2)解不等式组:$\left\{\begin{array}{l}{4x-3>2x-6①}\\{\frac{2}{5}-x≥-\frac{3}{5}②}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)根据整式混合运算的法则先算乘法,再算加减即可;
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:(1)原式=1-x2+x2+2x-1
=2x;
(2)由①得,x>-$\frac{3}{2}$,由②得,x≤1,
故不等式的解集为:-$\frac{3}{2}$<x≤1.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
20.观察下列关于x的单项式,探究其规律:2x,4x2,6x3,8x4,10x5,12x6,…,按照上述规律,第2016个单项式是( )
| A. | 2016x2015 | B. | 2016x2016 | C. | 4032x2015 | D. | 4032x2016 |
 如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$.
如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A′BC′,连接A′C,则A′C的长为4+3$\sqrt{3}$. 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.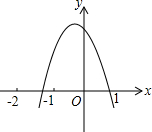 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )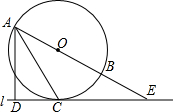 如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.