题目内容
1.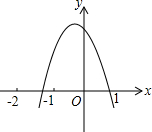 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 看图,当x=-2时,由函数值可得出结论①正确,由对称轴大于-1可知②正确,将点(-1,2)代入y=ax2+bx+c中得出a、b、c的数量关系,再根据对称轴大于-1得到不等式,将此不等式变形后知结论③正确,由a<0,对称轴小于0可知b<0,由抛物线交y的正半轴,可知c>0,即可判定④正确.
解答 解:当x=-2时,函数值小于0,
即4a-2b+c<0,故①正确;
由-2<x1<-1,0<x2<1,可知对称轴x=-$\frac{b}{2a}$>-1,且a<0,
∴2a<b,即2a-b<0,故②正确;
将点(-1,2)代入y=ax2+bx+c中,得a-b+c=2,即c=2-a+b,
由图象可知对称轴x=-$\frac{b}{2a}$>-1得2a-b<0,则(2a-b)2>0,
即b2>-4a2+4ab,
∴b2+8a>8a-4a2+4ab=4a(2-a+b)=4ac,
故③正确;
由图象可知,抛物线开口向下,∴a<0,对称轴x=-$\frac{b}{2a}$<0,∴b<0,
抛物线交y的正半轴,∴c>0,∴abc>0,故④正确.
故选D.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11. 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
 如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 完成下列各题:
完成下列各题: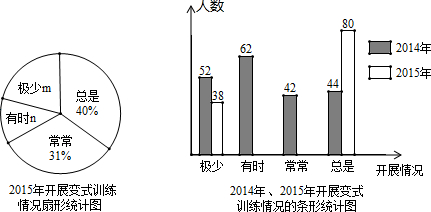
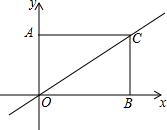 有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.
有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.