题目内容
13．2tan60°，$\sqrt{8}$，$\root{3}{16}$，π这四个实数中，最大的数是（ ）| A． | 2tan60° | B． | $\sqrt{8}$ | C． | $\root{3}{16}$ | D． | π |
分析 直接利用特殊角的三角函数值，以及利用平方根和立方根的定义化简求出答案．
解答 解：∵2tan60°=2$\sqrt{3}$≈3.46，$\sqrt{8}$=2$\sqrt{2}$≈2.8，2＜$\root{3}{16}$＜3，π≈3.14，
∴这四个实数中，最大的数是2tan60°．
故选：A．
点评 此题主要考查了实数比较大小以及特殊角的三角函数值，正确化简各数是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
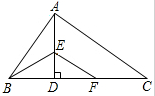如用，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论中：①AB=BF；②AE=ED；③AD=DC；④∠ABE=∠DFE；⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$，正确的是（ ）
如用，Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论中：①AB=BF；②AE=ED；③AD=DC；④∠ABE=∠DFE；⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$，正确的是（ ）| A． | ①③ | B． | ①⑤ | C． | ③④ | D． | ①②⑤ |
4．
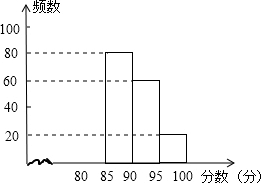某校组织了“安全在我心中”知识竞赛活动．根据获奖同学在竞赛中的成绩制成的统计图表如下：
根据以上图表提供的信息，解答下列问题：
（1）求出表中a、b、c的数值，并补全频数分布直方图；
（2）如果成绩在95分以上（含95分）的可以获得特等奖，那么获奖的同学获得特等奖的概率是多少？
（3）获奖成绩的中位数落在哪个分数段？并估算全部获奖同学的平均分．
某校组织了“安全在我心中”知识竞赛活动．根据获奖同学在竞赛中的成绩制成的统计图表如下：| 分数段 | 频数 | 频率 |
| 80≤x＜85 | a | 0.2 |
| 85≤x＜90 | 80 | b |
| 90≤x＜95 | 60 | c |
| 95≤x＜100 | 20 | 0.1 |
（1）求出表中a、b、c的数值，并补全频数分布直方图；
（2）如果成绩在95分以上（含95分）的可以获得特等奖，那么获奖的同学获得特等奖的概率是多少？
（3）获奖成绩的中位数落在哪个分数段？并估算全部获奖同学的平均分．
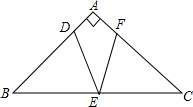如图，△ABC是等腰直角三角形，∠A=90°，点D为AB边上一点，E为BC的中点，将线段DE绕点E顺时针旋转45°后与AC交于点F．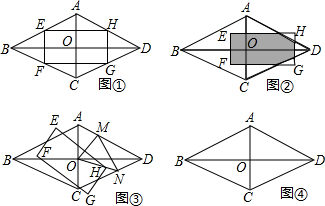
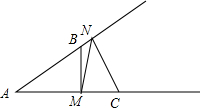已知∠BAC=30°，AB=3，AC=4，M在AC上，N在AB上，则BM+MN+NC的最小值是$\frac{3}{2}$+2$\sqrt{3}$．