题目内容
8.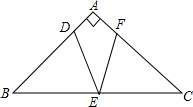 如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.
如图,△ABC是等腰直角三角形,∠A=90°,点D为AB边上一点,E为BC的中点,将线段DE绕点E顺时针旋转45°后与AC交于点F.(1)作出点F;(保留作图痕迹,不写作法和证明)
(2)若BC=4,BD=$\frac{3}{2}$$\sqrt{2}$,求CF的长.
分析 (1)作∠CEF=∠BDE交AC于F,利用等腰直角三角形的性质和三角形的外角性质可得∠DEF=45°;
(2)证明△BDE∽△CEF,然后利用相似比可计算出CF的长.
解答 解:(1)如图,点F为所作;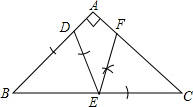
(2)∵△ABC是等腰直角三角形,
∴∠B=∠C=45°,
∵∠BDE=∠CEF,
∴△BDE∽△CEF,
∴BE:CF=BD:CE,即2:CF=$\frac{3\sqrt{2}}{2}$:2,
∴CF=$\frac{4\sqrt{2}}{3}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.解决(2)小题的关键是证明△BDE∽△CEF.

练习册系列答案
相关题目
13.2tan60°,$\sqrt{8}$,$\root{3}{16}$,π这四个实数中,最大的数是( )
| A. | 2tan60° | B. | $\sqrt{8}$ | C. | $\root{3}{16}$ | D. | π |
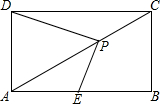 如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.
如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.