题目内容
9.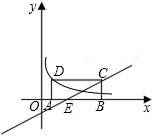 如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式.
如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式.
分析 由一次函数图象上点的坐标特征,即可求得点C的坐标,再根据矩形的性质,易得点D的坐标,所以把点D的坐标代入双曲线解析式,即可求得双曲线的表达式.
解答 解:根据矩形的性质知,点C的纵坐标是y=1,
∵y=$\frac{1}{2}$x-1经过点C,
∴1=$\frac{1}{2}$x-1,
解得x=4,
即点C的坐标是(4,1),
∵矩形ABCD在第一象限,AB在x轴正半轴上,AB=3,BC=1,
∴CD=4-3=1,
∴D(1,1),
∵双曲线y=$\frac{k}{x}$经过点D,
∴k=xy=1×1=1,
故双曲线的表达式为y=$\frac{1}{x}$.
点评 本题属于反比例函数与一次函数的交点问题,主要考查了一次函数以及反比例函数图象上点的坐标特征.解决问题的关键是利用了“矩形的对边相等,四个角都是直角的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.估计$\sqrt{16}$+$\sqrt{20}$的运算结果应在( )
| A. | 6与7之间 | B. | 7与8之间 | C. | 8与9之间 | D. | 9与10之间 |
17. 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )| A. | k1+k2 | B. | k1-k2 | C. | k1•k2 | D. | k1•k2-k2 |
4. 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )| A. | 4 | B. | 5 | C. | 10 | D. | 12 |
14.已知点P的坐标为(m,n),若m、n满足(m-n)2=m2+n2-4,则点P所在的象限是( )
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、三象限 |
1. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
18.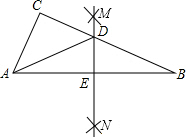 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )| A. | 3.5 | B. | 5 | C. | 7 | D. | 8 |
19.若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
| A. | 二次函数的图象与x轴的交点位于y轴的两侧 | |
| B. | 二次函数的图象与x轴的交点位于y轴的右侧 | |
| C. | 其中二次函数中的c>1 | |
| D. | 二次函数的图象与x轴的一个交于位于x=2的右侧 |
