题目内容
19.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位,用实数加法表示为3+(-2)=1.若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}. 解决问题:
(1)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C.再按照“平移量”{3,1}平移,最后的位置还是点B吗?在图①中画出四边形OABC,并求出该四边形的面积;
(2)如图②,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.

分析 (1)根据题中给出的平移量找出各对应点,描出各点,顺次连接即可.从两次平移量得出点的坐标一样,即可得出结论,最后用面积的和差求解即可;
(2)根据题中的文字叙述列出式子,计算即可.
解答 解:(1)作出如图1所示的图形,
Ⅰ、∵先把动点P按照“平移量”{3,1}平移到A,
∴A(3,1),
∵A再按照“平移量”{1,2}平移到B,
∴{3,1}+{1,2}={3+1,1+2}={4,3},
∴B(4,3),
Ⅱ、先把动点P按照“平移量”{1,2}平移到C,
∴C(1,2),
∵C再按照“平移量”{3,1}平移
∴{1,2}+{3,1}={1+3,2+1}={4,3}.
∴C再按照“平移量”{3,1}平移到的点坐标为(4,3)与B的坐标相同,
∴最后的位置仍是B.
∵A(3,1),B(4,3),C(1,2),
∴S四边形OABC=3×4-$\frac{1}{2}$×1×2-1×1-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3-1×1=6.
(2)从O出发,先向右平移2个单位,再向上平移3个单位,可知平移量为{2,3},
同理得到P到Q的平移量为{3,2},从Q到O的平移量为{-5,-5},
故有{2,3}+{3,2}+{-5,-5}={0,0}.
点评 此题几何变换综合题,主要考查了新定义“平移量”和平移量”间的加法运算法则,解本题的关键是理解定义和加法法则的基础上应用它,比较有创新,让学生在做题的同时又学到新知识,是一道考查了学生的阅读能力和理解能力的好题.

练习册系列答案
相关题目
2. 如图,下列能判断BC∥ED的条件是( )
如图,下列能判断BC∥ED的条件是( )
 如图,下列能判断BC∥ED的条件是( )
如图,下列能判断BC∥ED的条件是( )| A. | $\frac{ED}{BC}$=$\frac{AD}{AB}$ | B. | $\frac{ED}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{AC}{AE}$ |
 如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠ECD=70°,则∠BOD的度数为140°.
如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠ECD=70°,则∠BOD的度数为140°. 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置.

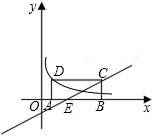 如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式.
如图,矩形ABCD整体位于在第一象限,且点A、B在x轴正半轴上,AB=3,BC=1,直线y=$\frac{1}{2}$x-1经过点C交x轴于点E,双曲线经过点D,求此双曲线的表达式.