题目内容
15.某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?
(3)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润不低于8000元?

分析 (1)根据图表中的信息可以在平面直角坐标系中描出相应的点,根据描出的点可以猜测该函数为一次函数,然后根据表格中的数据可以求出函数的解析式;
(2)根据题意可以列出相应的方程,从而可以解答本题;
(3)根据题意可以得到利润与售价之间的函数关系式,然后化为顶点式即可求得函数的最值,然后根据当地物价部门规定,该工艺品销售单价最高不能超过45元/件,工艺厂试销该工艺品每天获得的利润不低于8000元可以列出相应的不等式,从而可以解答本题.
解答 解:(1)如图所示,
由图可猜想y与x是一次函数关系,
设这个一次函数为y=kx+b(k≠0)
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴$\left\{\begin{array}{l}{500=30k+b}\\{400=40k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-10}\\{b=800}\end{array}\right.$,
∴函数关系式是:y=-10x+800;
(2)由题意可得,
(x-20)(-10x+800)=8000,
解得,x1=40或x2=60,
即当销售单价定为40或60元时,工艺厂试销该工艺品每天获得的利润为8000元;
(3)设工艺厂试销该工艺品每天获得的利润是W元,
依题意得 W=(x-20)(-10x+800)
=-10x 2+1000x-16000
=-10(x-50)2+9000,
∴当x=50时,W有最大值9000,
∴当销售单价定为50元/件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元,
当-10(x-50)2+9000≥8000时,得40≤x≤60,
∵当地物价部门规定,该工艺品销售单价最高不能超过45元/件,
∴那么销售单价定为40到45元时,工艺厂试销该工艺品每天获得的利润不低于8000元.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式和方程,根据二次函数的顶点式,会求函数的最值.

 阅读快车系列答案
阅读快车系列答案| 班级 | 考试人数 | 平均分 | 中位数 | 众数 | 方差 |
| 一班 | 51 | 80 | 84 | 88.78 | 186 |
| 二班 | 51 | 80 | 86 | 78 | 161 |
| A. | 一班、二班学生成绩的平均数相同 | |
| B. | 二班优生多于一班(优生为85分或85分以上者) | |
| C. | 二班成绩比一班整齐 | |
| D. | 成绩为78分的学生二班比一班多 |
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
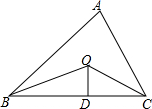 如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$.
如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$. 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③.
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③. 在Rt△ABC中,∠A=90°,
在Rt△ABC中,∠A=90°,