题目内容
5.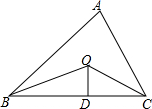 如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$.
如图,已知△ABC的周长是29,OB,OC分别平分∠ABC和∠ACB,OD⊥BC,垂足为D,且OD=3,则△ABC的面积是$\frac{87}{2}$.
分析 根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等(即OE=OD=OF),从而可得到△ABC的面积等于周长的一半乘以3,代入求出即可.
解答 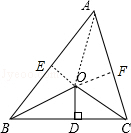 解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
解:如图,连接OA,过O作OE⊥AB于E,OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,
∴OE=OF=OD=3,
∵△ABC的周长是29,OD⊥BC于D,且OD=3,
∴S△ABC=$\frac{1}{2}$×AB×OE+$\frac{1}{2}$×BC×OD+$\frac{1}{2}$×AC×OF
=$\frac{1}{2}$×(AB+BC+AC)×3
=$\frac{1}{2}$×29×3=$\frac{87}{2}$,
故答案为:$\frac{87}{2}$.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.二次函数y=2(x-3)2+5的图象的顶点坐标为( )
| A. | (3,5) | B. | (3,-5) | C. | (-3,5) | D. | (-3,-5) |
13.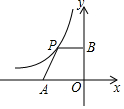 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
 如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )
如图,平面直角坐标系中,点A是x轴负半轴上一个定点,点P是函数y=$\frac{-6}{x}$(x<0)上一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会( )| A. | 先增后减 | B. | 先减后增 | C. | 逐渐减小 | D. | 逐渐增大 |
10.下面四个等式的变形中正确的是( )
| A. | 由4x+8=0得x+2=0 | B. | 由x+7=5-3x得4x=2 | ||
| C. | 由$\frac{3}{5}$x=4得x=$\frac{12}{5}$ | D. | 由-4(x-1)=-2得4x=-6 |
14.下列说法正确的是( )
| A. | -x2y-22x3y是六次多项式 | B. | $\frac{3x+y}{3}$是单项式 | ||
| C. | -$\frac{1}{2}$πab的系数是-$\frac{1}{2}$π,次数是2次 | D. | $\frac{1}{a}$+1是多项式 |
15.某工艺厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?
(3)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润不低于8000元?

| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为8000元?
(3)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润不低于8000元?

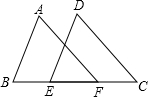 如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).
如图,若AB=DE,BE=CF,要证△ABF≌△DEC,需补充条件AF=DC(填写一个即可).