题目内容
20.正六边形的边长是2,则此正六边形的半径为2,边心距为$\sqrt{3}$,面积为6$\sqrt{3}$.分析 首先根据题意作出图形,然后可得△OBC是等边三角形,然后由三角函数的性质,求得OH的长,继而求得正六边形的面积.
解答 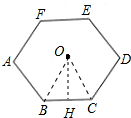 解:如图,连接OB,OC,过点O作OH⊥BC于H,
解:如图,连接OB,OC,过点O作OH⊥BC于H,
∵六边形ABCDEF是正六边形,
∴∠BOC=$\frac{1}{6}$×360°=60°,
∵OB=0C,
∴△OBC是等边三角形,
∴BC=OB=OC=2,
∴它的半径为2,边长为2;
∵在Rt△OBH中,OH=OB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴边心距是:$\sqrt{3}$;
∴S正六边形ABCDEF=6S△OBC=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$.
故答案为:2,$\sqrt{3}$,6$\sqrt{3}$.
点评 本题考查了圆的内接正六边形的性质、正多边形的内角和、等边三角形的判定与性质以及三角函数等知识.此题难度不大,注意掌握数形结合思想的应用

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.一种商品按销售量分三部分制定销售单价.如下表:
(1)若买100件花250元,买300件花690元.
(2)小明买这种商品花了n元.解决下列问题:
①小明买了这种商品多少件(用n的式子表示);
②如果小明买这种商品的件数恰好是0.45n件,求n的大小.
| 销售量 | 单价 |
| 不超过100件的部分 | 2.5元/件 |
| 超过100件不超过300件的部分 | 2.2元/件 |
| 超过300件的部分 | 2元/件 |
(2)小明买这种商品花了n元.解决下列问题:
①小明买了这种商品多少件(用n的式子表示);
②如果小明买这种商品的件数恰好是0.45n件,求n的大小.
7.下列方程中是一元二次方程的是( )
| A. | (x-1)(3+x)=5 | B. | x2+$\frac{1}{x}$-$\frac{9}{2}$=0 | C. | y2+2x+4=0 | D. | 4x2=(2x-1)2 |
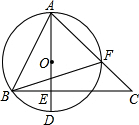 变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?
变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?