题目内容
9．
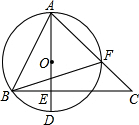变式：如图，AD是⊙O的直径，AD⊥BC，△ABF与△ACB相似吗？
分析 先利用垂直的定义得到∠C+∠CAE=90°，再根据圆周角定理，由AD为直径得到∠AFD=90°，则∠ADF+∠DAF=90°，则利用等角的余角相等得∠ADF=∠C，然后根据圆周角定理可得∠ABF=∠ADF，得出∠C=∠ABF，再由公共角，即可得出结论．
解答 解：△ABF∽△ACB．理由如下：
连结DF，如图所示，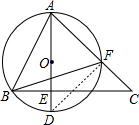
∵AD⊥BC，
∴∠C+∠CAE=90°，
∵AD为直径，
∴∠AFD=90°，
∴∠ADF+∠DAF=90°，
∴∠ADF=∠C，
∵∠ABF=∠ADF，
∴∠C=∠ABF，
∵∠BAF=∠CAB，
∴△ABF∽△ACB．
点评 本题考查了相似三角形的判定方法、圆周角定理；熟练掌握相似三角形的判定方法，证出∠C=∠ABF是解决问题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
如图，AB是⊙O的直径，点C在⊙O上，∠AOC=40°，D是$\widehat{BC}$的中点，求∠ACD的度数．
如图所示，在△ABC中，BD，CD分别为∠ABC，∠ACB外角平分线，则∠D与∠A有什么关系，并说明理由．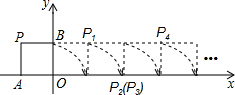
如图，将边长为1的正方形OAPB沿x轴正方向连续翻转48次，点P依次落在点P1，P2，P3，P4，…，P48的位置，则P48的坐标是（47，1）．