题目内容
12. 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )| A. | $\sqrt{2}-3$ | B. | 2$\sqrt{2}$-1 | C. | 3$\sqrt{2}$-3 | D. | 2-$\sqrt{2}$ |
分析 根据中点坐标公式,可得x的值,根据绝对值的性质,分母有理化,可得答案.
解答 解:由题意,得
$\sqrt{2}$+x=2,
解得x=2-$\sqrt{2}$.
|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$=|2-$\sqrt{2}$-$\sqrt{2}$|+$\frac{2-\sqrt{2}}{\sqrt{2}}$
=2$\sqrt{2}$-2+$\sqrt{2}$-1
=3$\sqrt{2}$-3,
故选:C.
点评 本题考查了实数与数轴,利用中点坐标公式得出x的值是解题关键.

练习册系列答案
相关题目
2.泸溪三口岩水库移民新村分给小慧家一套价格为12万元的住房,按要求,需首期(第一年)付房款3万元,从第二年起,每年应付房款0.5万元与上一年剩余房款的利息的和,假设剩余房款年利率为0.4%,小慧列表推算如下:
若第n年小慧家仍需还款,则第n年应还款0.54-0.002n万元(用含n的代数式表示,n>1).
| 第一年 | 第二年 | 第三年 | … | |
| 应还款(万元) | 3 | 0.5+9×0.4% | 0.5+8.5×0.4% | … |
| 剩余房款(万元) | 9 | 8.5 | 8 | … |
13.已知sinB=$\frac{\sqrt{2}}{2}$,则∠B等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
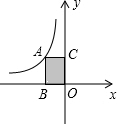 如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )
如图所示,设A为反比例函数y=$\frac{k}{x}$图象上一点,且矩形ABOC的面积为3,则k的值为( )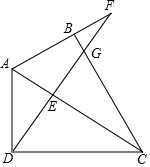 如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF. 如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?
如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?