题目内容
20．2-$\sqrt{5}$的绝对值是$\sqrt{5}$-2；当x≥-1时，式子$\sqrt{x+1}$有意义．分析 根据差的绝对值是大数减小数，可得答案；
根据二次根式的被开方数是非负数，可得答案．
解答 解：|2-$\sqrt{5}$|=$\sqrt{5}$-2，
要使式子$\sqrt{x+1}$有意义，得
x+1≥0．
解得x≥-1，
故答案为：$\sqrt{5}$-2，≥-1．
点评 本题考查了实数的性质，差的绝对值是大数减小数，二次根式有意义的条件是被开方数是非负数．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
18．
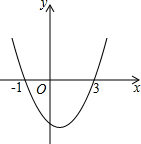已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0），对于下列结论不正确的是（ ）
已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0），对于下列结论不正确的是（ ）| A． | b2-4ac＞0 | B． | b+2a=0 | C． | abc＞0 | D． | 8a+c＜0 |
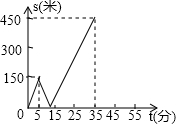甲、乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象的一部分如图所示．
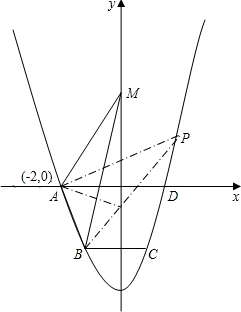如图，抛物线y=ax2+c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，A点到原点的距离为2，梯形的高为3，C点到y轴的距离为1，
5．在代数式$\frac{x}{3x+1}$、-$\frac{{x}^{2}+1}{3}$、$\frac{x}{2}$-y2、$\frac{a-2b}{a+2}$、$\frac{{a}^{2}}{2a}$、$\frac{a}{π}$中，分式的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．下列运算正确的是（ ）
| A． | （-x2）3=-x5 | B． | x2•x4=x8 | C． | x3+x3=2x3 | D． | （x-y）2=x2-y2 |
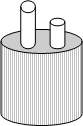如图，两根铁棒直立于桶底水平的木桶中，在桶中加入水后，一根露出水面的长度是它的$\frac{1}{3}$，另一根露出水面的长度是它的$\frac{1}{5}$，两根铁棒长度之和为220cm，求两根铁棒的长度．
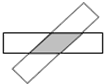如图，将两张长为9，宽为3的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的面积有最小值9，那么菱形面积的最大值是15．