题目内容
5．在代数式$\frac{x}{3x+1}$、-$\frac{{x}^{2}+1}{3}$、$\frac{x}{2}$-y2、$\frac{a-2b}{a+2}$、$\frac{{a}^{2}}{2a}$、$\frac{a}{π}$中，分式的个数是（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．
解答 解：$\frac{x}{3x+1}$是分式、-$\frac{{x}^{2}+1}{3}$不是分式、$\frac{x}{2}$-y2不是分式、$\frac{a-2b}{a+2}$是分式、$\frac{{a}^{2}}{2a}$是分式、$\frac{a}{π}$不是分式，
故选C．
点评 本题主要考查分式的定义，注意π不是字母，是常数．
练习册系列答案
阅读快车系列答案
相关题目
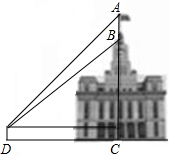如图，某建筑物BC上有一旗杆AB，从与BC相距38m的D处观测旗杆顶部A的仰角为50°，观测旗杆底部B的仰角为45°，则旗杆的高度约为7.2m．（结果精确到0.1m，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）
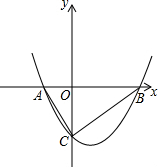一个二次函数的图象上任一点的坐标（x，y）满足方程$\sqrt{（x-\frac{3}{2}）^{2}+（y+\frac{21}{8}）^{2}}$=|y+$\frac{29}{8}$|．
10．某厂1月份生产原料a吨，以后每个月比前一个月增产x%，3月份生产原料的吨数是（ ）
| A． | a（1+x）2 | B． | a（1+x%）2 | C． | a+a•x% | D． | a+a•（x%）2 |
15．若$\frac{1}{2}{x^{a-1}}{y^{2b}}$与$-\frac{1}{3}{x^{2-b}}{y^2}$是同类项，则a、b值分别为（ ）
| A． | a=2，b=-1 | B． | a=2，b=1 | C． | a=-2，b=1 | D． | a=-2，b=-1 |