题目内容
18.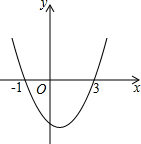 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论不正确的是( )| A. | b2-4ac>0 | B. | b+2a=0 | C. | abc>0 | D. | 8a+c<0 |
分析 A:根据图示,可得ax2+bx+c=0有两个不同的实数根,所以△>0,即b2-4ac>0,据此判断即可;
B:根据ax2+bx+c=0的两个不同的实根是-1、3,可得$-\frac{b}{a}=-1+3=2$,所以b+2a=0,据此判断即可;
C:首先根据二次函数的图象开口向上,可得a>0;然后根据对称轴在y轴的右边,可得$-\frac{b}{2a}$>0,所以b<0;最后根据二次函数与y轴的交点在y轴的下方,可得
c<0,所以abc>0,据此判断即可;
D:首先根据ax2+bx+c=0的两个不同的实根是-1、3,可得$\frac{c}{a}=(-1)×3=-3$,所以3a+c=0,然后根据a>0,判断出8a+c>0即可.
解答 解:∵ax2+bx+c=0有两个不同的实数根,
∴△>0,
∴b2-4ac>0,
∴选项A正确.
∵ax2+bx+c=0的两个不同的实根是-1、3,
∴$-\frac{b}{a}=-1+3=2$,
∴b+2a=0,
∴选项B正确.
∵二次函数的图象开口向上,
∴a>0;
∵$-\frac{b}{2a}$>0,a>0,
∴b<0;
∵二次函数与y轴的交点在y轴的下方,
∴c<0,
∴abc>0,
∴选项C正确.
∵ax2+bx+c=0的两个不同的实根是-1、3,
∴$\frac{c}{a}=(-1)×3=-3$,
∴3a+c=0,
又∵a>0,
∴5a>0,
∴5a+(3a+c)>0,
即8a+c>0,
∴选项D错误.
故选:D.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

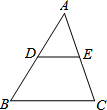 如图,DE是△ABC的中位线,若BC的长是12cm,则DE的长是6cm.
如图,DE是△ABC的中位线,若BC的长是12cm,则DE的长是6cm.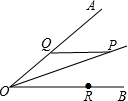 如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10.
如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10.
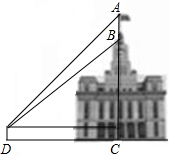 如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度约为7.2m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1、2、3、4、…、20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为( )
如图,以点O为圆心的20个同心圆,它们的半径从小到大依次是1、2、3、4、…、20,阴影部分是由第1个圆和第2个圆,第3个圆和第4个圆,…,第19个圆和第20个圆形成的所有圆环,则阴影部分的面积为( ) 如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.
如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.