题目内容
8.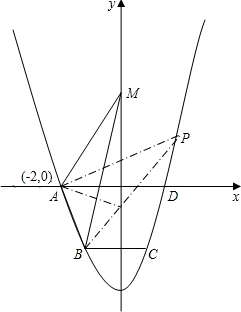 如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,A点到原点的距离为2,梯形的高为3,C点到y轴的距离为1,(1)求抛物线的解析式;
(2)点M为y轴上的任意一点,求点M到A,B两点的距离之和的最小值及此时点M的坐标;
(3)在第(2)的结论下,抛物线上的P的使S△PAD=S△ABM成立,求点P的坐标.
分析 (1)易知A(-2,0),C(1,-3),将A、C两点的坐标代入y=ax2+c,利用待定系数法即可求出抛物线的解析式;
(2)由于A、D关于抛物线对称轴即y轴对称,那么连接BD,BD与y轴的交点即为所求的M点,可先求出直线BD的解析式,即可得到M点的坐标;
(3)设直线BC与y轴的交点为N,那么S△ABM=S梯形AONB-S△BMN-S△AOM,由此可求出△ABM和△PAD的面积;在△PAD中,AD的长为定值,可根据其面积求出P点纵坐标的绝对值,然后代入抛物线的解析式中即可求出P点的坐标.
解答 解:(1)由题意可得:A(-2,0),C(1,-3),
∵抛物线y=ax2+c(a>0)经过A、C两点,
∴$\left\{\begin{array}{l}{4a+c=0}\\{a+c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{c=-4}\end{array}\right.$,
∴抛物线的解析式为:y=x2-4;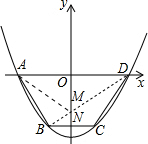 (2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD,则BD与y轴的交点即为M点;
(2)由于A、D关于抛物线的对称轴(即y轴)对称,连接BD,则BD与y轴的交点即为M点;
设直线BD的解析式为:y=kx+b(k≠0),
∵B(-1,-3),D(2,0),
∴$\left\{\begin{array}{l}{-k+b=-3}\\{2k+b=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$,
∴直线BD的解析式为y=x-2,
当x=0时,y=-2,
∴点M的坐标是(0,-2);
(3)设BC与y轴的交点为N,则有N(0,-3),
∵M(0,-2),B(-1,-3),
∴MN=1,BN=1,ON=3,
∴S△ABM=S梯形AONB-S△BMN-S△AOM=$\frac{1}{2}$(1+2)×3-$\frac{1}{2}$×1×1-$\frac{1}{2}$×2×2=2,
∴S△PAD=S△ABM=2.
∵S△PAD=$\frac{1}{2}$AD•|yP|=2,AD=4,
∴|yP|=1.
当P点纵坐标为1时,x2-4=1,解得x=±$\sqrt{5}$,
∴P1($\sqrt{5}$,1),P2(-$\sqrt{5}$,1);
当P点纵坐标为-1时,x2-4=-1,解得x=±$\sqrt{3}$,
∴P3($\sqrt{3}$,-1),P4(-$\sqrt{3}$,-1);
故存在符合条件的P点,且P点坐标为:P1($\sqrt{5}$,1),P2(-$\sqrt{5}$,1),P3($\sqrt{3}$,-1),P4(-$\sqrt{3}$,-1).
点评 此题是二次函数的综合题型,其中涉及到二次函数解析式的确定、函数图象交点及图形面积的求法,轴对称的性质等.当所求图形不规则时,一般要将不规则图形转换为几个规则图形面积的和差来求.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案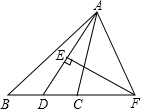 如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )
如图,在△ABC中,∠ABC=45°,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于F,则∠CAF的度数是( )| A. | 30° | B. | 45° | C. | 75° | D. | 60° |
| A. | 30x-8=31x+26 | B. | 30x+8=31x+26 | C. | 30x-8=31x-26 | D. | 30x+8=31x-26 |
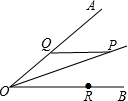 如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10.
如图所示,∠AOB=30°,角内有点P,PO=10cm,两边上各有一点Q,R(均不同于点O),则△PQR的周长最小值是10. 如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.
如图,已知点A,C在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,D在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=3,CD=2,AB与CD的距离为5,则a-b的值是6.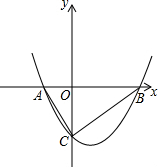 一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.
一个二次函数的图象上任一点的坐标(x,y)满足方程$\sqrt{(x-\frac{3}{2})^{2}+(y+\frac{21}{8})^{2}}$=|y+$\frac{29}{8}$|.