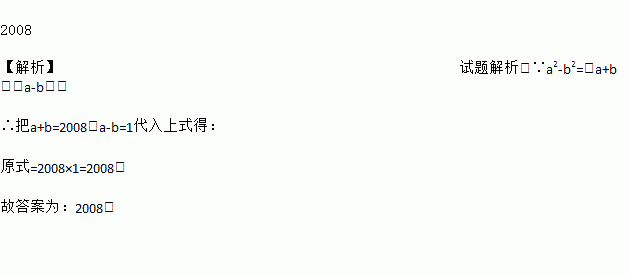题目内容
如果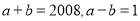 ,那么
,那么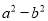 =___________.
=___________.
 2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008.
2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008.
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
掷一枚正方体的骰子,各个面上分别标有数字1, 2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字不是3的倍数;
④朝上的数字小于6;
⑤朝上的数字不小于3.
 ①;②;③;④;⑤
【解析】试题分析:本题考察可能性大小的应用,关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,是奇数点的有3种可能,故其频率是;
②【解析】
一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,...
①;②;③;④;⑤
【解析】试题分析:本题考察可能性大小的应用,关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,每一个点数出现的频率相同.其中,是奇数点的有3种可能,故其频率是;
②【解析】
一枚质地均匀的正方体的骰子,抛掷落地后,可能出现朝上的面的点数是:1,2,3,4,5,6,... 如图,在锐角三角形ABC中,∠BAC=60°,边AC、AB的垂直平分线交于点O,交AC、AB于点D、E,则∠BOC等于____.
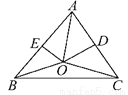
 120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是:120°.
120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是:120°. 正方形既是_________图形,又是_____________图形
 轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案:轴对称,中心对称.
轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案:轴对称,中心对称. 如图,不是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 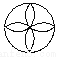
 B
【解析】根据中心对称的定义可以知道B选项不是中心对称图形.故选B.
B
【解析】根据中心对称的定义可以知道B选项不是中心对称图形.故选B. 把下列各式分解因式:
(1)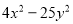 (2)
(2) 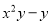
(3)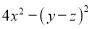 (4)
(4)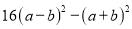
(5)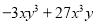 (6)
(6) 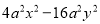
(7) 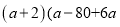 (8)
(8) 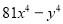
(9) 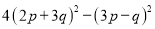 (10)
(10) 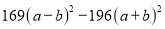
 (1)(2x+5y)(2x-5y); (2)y(x+1)(x-1); (3)(2x+y-z)(2x-y+z); (4)(5a-3b)(3a-5b);
(5)-3xy(y+3x)(y-3x); (6)4a2(x+2y)(x-2y); (7)(a+4)(a-4); (8) ;
(9)(7p+5q)(p+7q); (10)-(27a+b)(a+27b);.
【解析】试题分析:(1)直接...
(1)(2x+5y)(2x-5y); (2)y(x+1)(x-1); (3)(2x+y-z)(2x-y+z); (4)(5a-3b)(3a-5b);
(5)-3xy(y+3x)(y-3x); (6)4a2(x+2y)(x-2y); (7)(a+4)(a-4); (8) ;
(9)(7p+5q)(p+7q); (10)-(27a+b)(a+27b);.
【解析】试题分析:(1)直接... 若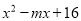 是完全平方式,那么m=________.
是完全平方式,那么m=________.
 ±8
【解析】试题解析:∵若x2-mx+16是一个完全平方式,
∴m=±8,
故答案为:±8
±8
【解析】试题解析:∵若x2-mx+16是一个完全平方式,
∴m=±8,
故答案为:±8 在平面直角坐标系中,点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,则A′B′可表示为 .
 x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3).
x=-1(-2≤y≤3).
【解析】
试题解析:∵点A的坐标是(2,3),点B的坐标是(2,-2),若把线段AB向左平移3个单位后变为A′B′,
∴点A′的坐标为(-1,3);点B′的坐标为(-1,-2),
∴线段A′B′可表示为 x=-1(-2≤y≤3). 已知二次函数y=x2+bx-2的图象与x轴的一个交点为(1,0),则它与x轴的另一个交点坐标是( )
A. (1,0) B. (2,0) C. (-2,0) D. (-1,0)
 C
【解析】试题分析:把x=1,y=0代入y=x2+bx-2得:
0=1+b-2,
∴b=1,
∴对称轴为x==,
∴x==,
∴x2=-2,
它与x轴的另一个交点坐标是(-2,0).
故选C.
C
【解析】试题分析:把x=1,y=0代入y=x2+bx-2得:
0=1+b-2,
∴b=1,
∴对称轴为x==,
∴x==,
∴x2=-2,
它与x轴的另一个交点坐标是(-2,0).
故选C.