题目内容
判断对错：轴对称图形也是中心对称图形；__________________
错
【解析】有的图形是轴对称图形但不一定是中心对称图形，例如等腰三角形.
故答案：错.
练习册系列答案
相关题目
在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
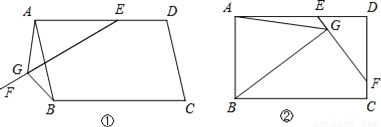
（1）证明见解析；（2）EG=AG﹣BG，理由见解析．
【解析】试题分析：（1）如图，作∠GAH=∠EAB交GE于点H，易证△ABG≌△AEH ，再判定△AGH是等边三角形，即可得结论；（2）EG=AG-BG，如图②，作∠GAH=∠EAB交GE于点H，类比（1）的方法证明△ABG≌△AEH，再判定△AGH是等腰直角三角形，即可得结论.
试题解析：
如图，作∠GAH=∠EAB交GE... 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使AE+CD=AD．连结CE，求证：CE平分∠BCD．
证明见解析．
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，AD=BC，由平行线的性质得出∠E=∠DCE，由已知条件得出BE=BC，由等腰三角形的性质得出∠E=∠BCE，得出∠DCE=∠BCE即可．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD=BC，∴∠E=∠DCE，∵AE+CD=AD，∴BE=BC，∴∠E=∠BCE，∴∠DCE=∠BCE，... 如图，在锐角三角形ABC中，∠BAC＝60°，边AC、AB的垂直平分线交于点O，交AC、AB于点D、E，则∠BOC等于____.
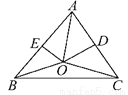
120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是：120°. 中心对称图形和旋转对称图形的区别是什么呢？
见解析
【解析】【试题分析】注意从定义上区别.
【试题解析】中心对称是把一个图形绕其几何中心旋转180度后能够和原来的图形互相重合的图形叫中心对称图形.这个点就是它的对称中心．例如菱形；旋转对称不是旋转一定的角度，而是旋转非周角的角度。就是说不能是旋转360度的整数倍后与自身重合了。例如电扇的叶片转动120°与自身重合，当然菱形也是旋转对称，但并不是所有的旋转对称都是中心对称.
... 正方形既是_________图形，又是_____________图形
轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案：轴对称，中心对称. 如图，不是中心对称图形的是（ ）
A. 
B. 
C. 
D. 
B
【解析】根据中心对称的定义可以知道B选项不是中心对称图形.故选B. 若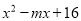
是完全平方式，那么m=________.
±8
【解析】试题解析：∵若x2-mx+16是一个完全平方式，
∴m=±8，
故答案为：±8 已知抛物线y= -x2+mx+（7-2m）（m为常数）．
（1）证明：不论m为何值，抛物线与x轴恒有两个不同的交点；
（2）若抛物线与x轴的交点A（x1，0）、B（x2，0）的距离为AB=4（A在B的左边），且抛物线交y轴的正半轴于C，求抛物线的解析式．
（1）证明见解析；（2）抛物线的解析式为y= -x2+2x+3．
【解析】试题分析：（1）要证明抛物线与x轴恒有两个不同的交点证明抛物线的判别式是正数，所以证明判别式是正数即可解决问题；
（2）首先由AB=4可以得|x2-x1|=4，而（x2-x1）2=（x2-x1）2-4x1x2=16，然后利用根与系数的关系即可得到关于m方程，解方程即可求出m，也就求出了抛物线的解析式．
试题...