题目内容
口袋中有9个球，其中4个红球，3个蓝球，2个白球，在下列事件中，发生的可能性为1的是（ ）
A. 从口袋中拿一个球恰为红球 B. 从口袋中拿出2个球都是白球
C. 拿出6个球中至少有一个球是红球 D. 从口袋中拿出的5个球恰为3红2白
C
【解析】对于A，从口袋中拿一个球恰为红球，可能性小于1,故不符合题意；
对于B，从口袋中拿出2个球都是白球，这是一个随机事件，发生的可能性小于1,故不符合题意；
对于C，拿出6个球中，至少有一个球是红球是正确的，因为蓝球3个，白球5个，如果在极端情况下，这6个球尽可能的不是红球，那么最多有五个不是红球，至少有一个是红球，所以C正确.
对于D, 从口袋中拿出的5个球恰为3...
阅读快车系列答案先化简，再求值: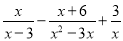 
，其中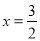
．
【解析】试题分析：第二个分母分解因式，找出最简公分母，通分加减，化成最简后代入x的值计算即可．
试题解析：
【解析】
原式＝
＝
＝
＝
＝，
当x＝时，
原式＝
＝． 在平行四边形ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．
（1）如图①，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；
（2）如图②，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．
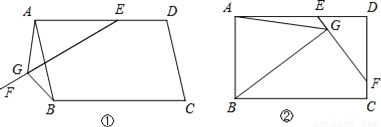
（1）证明见解析；（2）EG=AG﹣BG，理由见解析．
【解析】试题分析：（1）如图，作∠GAH=∠EAB交GE于点H，易证△ABG≌△AEH ，再判定△AGH是等边三角形，即可得结论；（2）EG=AG-BG，如图②，作∠GAH=∠EAB交GE于点H，类比（1）的方法证明△ABG≌△AEH，再判定△AGH是等腰直角三角形，即可得结论.
试题解析：
如图，作∠GAH=∠EAB交GE... 掷一枚正方体的骰子，各个面上分别标有数字1， 2，3，4，5，6，求下列事件发生的频率的大小：
①朝上的数字是奇数；
②朝上的数字能被3除余1；
③朝上的数字不是3的倍数；
④朝上的数字小于6；
⑤朝上的数字不小于3.
①；②；③；④；⑤
【解析】试题分析:本题考察可能性大小的应用，关键是推断出各色扑克被抽到的频率是多少.
①【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，每一个点数出现的频率相同.其中，是奇数点的有3种可能，故其频率是；
②【解析】
一枚质地均匀的正方体的骰子，抛掷落地后，可能出现朝上的面的点数是：1，2，3，4，5，6，... 同时掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能发生的事件是( )
A. 点数之和为12 B. 点数之和小于3 C. 点数之和大于4且小于8 D. 点数之和为13
D
【解析】试题分析：找到一定不会发生的事件即可．
【解析】
A、6点+6点=12点，为随机事件，不符合题意；
B、例如：1点+1点=2点，为随机事件，不符合题意；
C、例如：1点+5点=6点，为随机事件，不符合题意；
D、两枚骰子点数最大之和为12点，不可能是13点，为不可能事件，符合题意．
故选：D． 下列说法正确的是( )
A. 如果一件事情发生的可能性达到99.9999%，说明这件事必然发生；
B. 如果一事件不是不可能事件,说明此事件是不确定事件；
C. 可能性的大小与不确定事件有关；
D. 如果一事件发生的可能性为百万分之一，那么这事件是不可能事件.
C
【解析】试题分析：根据必然事件、不可能事件、不确定事件的概念依次分析即可.
A.如果一件事情发生的可能性达到99.9999%,说明这件事很可能发生，但仍然是不确定事件，故错误；
B.如果一事件不是不可能事件,说明此事件是不确定事件或必然事件，故错误；
C.可能性的大小与不确定事件有关，正确；
D.如果一事件发生的可能性为百万分之一，这事件是不确定事件，故错误；
... 已知：如图，四边形ABCD是平行四边形，延长BA至点E，使AE+CD=AD．连结CE，求证：CE平分∠BCD．
证明见解析．
【解析】试题分析：由平行四边形的性质得出AB∥CD，AB=CD，AD=BC，由平行线的性质得出∠E=∠DCE，由已知条件得出BE=BC，由等腰三角形的性质得出∠E=∠BCE，得出∠DCE=∠BCE即可．
试题解析：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，AD=BC，∴∠E=∠DCE，∵AE+CD=AD，∴BE=BC，∴∠E=∠BCE，∴∠DCE=∠BCE，... 如图，在锐角三角形ABC中，∠BAC＝60°，边AC、AB的垂直平分线交于点O，交AC、AB于点D、E，则∠BOC等于____.
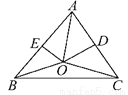
120°
【解析】∵AB,AC的垂直平分线交于点O,
∴OA=OB=OC
∴∠OAB=∠OBA,∠OAC=∠OCA
∴∠OAB+∠OAC=∠OBA+∠OCA=∠A=60°
∴∠OBC+∠OCB=180°-2*60°=60°
∴∠BOC=180°-60°=120°.
故答案是：120°. 若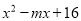
是完全平方式，那么m=________.
±8
【解析】试题解析：∵若x2-mx+16是一个完全平方式，
∴m=±8，
故答案为：±8