题目内容
8.点A(2,y1),B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2大大小关系为( )| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法判断 |
分析 本题需先根据已知条件求出二次函数的图象的对称轴,再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系.
解答 解:∵二次函数y=x2-2x+1的图象的对称轴是x=1,
在对称轴的右面y随x的增大而增大,
∵点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,
2<3,
∴y1<y2.
故选C.
点评 本题主要考查了二次函数图象上点的坐标特征,在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键

练习册系列答案
相关题目
18.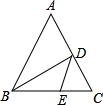 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
 如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )
如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为( )| A. | AD<DE | B. | AD=DE | C. | AD>DE | D. | 不确定 |
3.能使两个直角三角形全等的条件是( )
| A. | 两条边对应相等 | B. | 一条边对应相等 | C. | 一锐角对应相等 | D. | 两锐角对应相等 |
20.关于x的一元二次方程x2+bx+c=0的两个实数根分别为-2和3,则( )
| A. | b=1,c=-6 | B. | b=-1,c=-6 | C. | b=5,c=-6 | D. | b=-1,c=6 |
 如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点. 已知:如图,AD是△ABC的角平分线,且AD是△ABC的高,点E是BA延长线上一点,EG⊥BC,垂足为G,EG交AC于点F.求证:
已知:如图,AD是△ABC的角平分线,且AD是△ABC的高,点E是BA延长线上一点,EG⊥BC,垂足为G,EG交AC于点F.求证: 如图,已知AC⊥BD于点O,AB=DC,∠1=∠2.
如图,已知AC⊥BD于点O,AB=DC,∠1=∠2.