题目内容
抛物线y=2x2+8x-4与y轴的交点坐标是 .
考点:二次函数图象上点的坐标特征
专题:计算题
分析:求出自变量为0时的函数值即可.
解答:解:当x=0时,y=2x2+8x-4=-4,
所以抛物线y=2x2+8x-4与y轴的交点坐标为(0,-4).
故答案为(0,-4).
所以抛物线y=2x2+8x-4与y轴的交点坐标为(0,-4).
故答案为(0,-4).
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )| A、6 | B、8 | C、10 | D、12 |
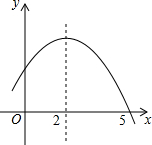 二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )
二次函数y=ax2+bx+c的部分图象如图所示,由图象可知方程ax2+bx+c=0的根是( )| A、x1=-1,x2=5 |
| B、x1=-2,x2=4 |
| C、x1=-1,x2=2 |
| D、x1=-5,x2=5 |
 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )| A、120° | B、100° |
| C、80° | D、60° |
在下列命题中,正确的是( )
| A、三点确定一个圆 |
| B、圆的内接等边三角形只有一个 |
| C、一个三角形有且只有一个外接圆 |
| D、一个四边形一定有外接圆 |
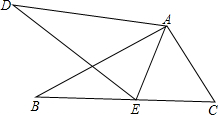 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件