题目内容
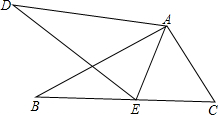 如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件
如图,∠CAE=∠DAB,AB=AD,请你再补充一个条件考点:全等三角形的判定
专题:
分析:首先根据∠CAE=∠DAB,可得∠DAE=∠BAC,再添加条件AE=AC可利用SAS定理判定△ABC≌△ADE.
解答:解:补充AE=AC,
∵∠CAE=∠DAB,
∴∠CAE+∠BAE=∠DAB+∠BAE,
即∠DAE=∠BAC,
在△BAC和△DAE中
,
∴△ABC≌△ADE(SAS).
故答案为:AE=AC.
∵∠CAE=∠DAB,
∴∠CAE+∠BAE=∠DAB+∠BAE,
即∠DAE=∠BAC,
在△BAC和△DAE中
|
∴△ABC≌△ADE(SAS).
故答案为:AE=AC.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
 如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D.
如图,⊙O1、⊙O2外切于点P,A是⊙O1上一点,直线AC切⊙O2于点C,交⊙O1于点B,直线AP交⊙O2于点D. 如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,CD=10,AB=20,求∠A的度数.
如图,△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,CD=10,AB=20,求∠A的度数.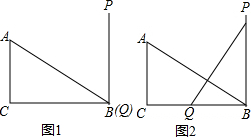 如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于
如图,在△ABC中,∠ACB=90°,BC=4,AC=3,线段PQ⊥BC于Q(如图,此时点Q与点B重合),PQ=AB,当点P沿PB向B滑动时,点Q相应的从B沿BC向C滑动,始终保持PQ=AB不变,当△ABC与△PBQ全等时,PB的长度等于 如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数是
如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠AMN+∠ANM的度数是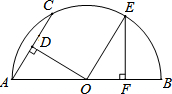 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=12,则OF的长为( ) 如图,?ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,求?ABCD的面积.
如图,?ABCD中,对角线AC、BD交于点O,若∠BOC=120°,AD=7,BD=10,求?ABCD的面积.