题目内容
17.若直角三角形的两直角边长为a,b,且满足$\sqrt{{a}^{2}-6a+9}$+|b-4|=0,则该直角三角形的斜边上的高为( )| A. | 5 | B. | 4 | C. | 2.4 | D. | 2 |
分析 根据非负数的性质得到a、b的值,然后结合勾股定理求得斜边的长度即可.
解答 解:∵$\sqrt{{a}^{2}-6a+9}$+|b-4|=0,
∴a2-6a+9=0,|b-4|=0,
∴a=3,b=4,
∴该直角三角形的斜边长为:$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴直角三角形的斜边上的高为$\frac{3×4}{5}$=2.4,
故选C.
点评 本题考查了勾股定理,非负数的性质-绝对值、算术平方根.任意一个数的绝对值(二次根式)都是非负数,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
9.一个直角三角形,有两边长分别为6和8,下列说法正确的是( )
| A. | 第三边为$2\sqrt{7}$ | B. | 三角形的周长为25 | ||
| C. | 三角形的面积为48 | D. | 第三边可能为10 |
6.已知直角三角形两边的长为3和4,则第三边的长为( )
| A. | 7 | B. | 5 | C. | 5或$\sqrt{7}$ | D. | 以上都不对 |
7.三角形三条中位线的长分别为5、12、13,则此三角形的面积为( )
| A. | 120 | B. | 240 | C. | 30 | D. | 60 |
 如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E、F分别为AC和AB的中点,则△AEF的周长等于( )
如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E、F分别为AC和AB的中点,则△AEF的周长等于( )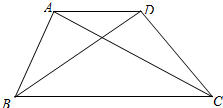 已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:
已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求: