题目内容
2.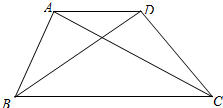 已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:
已知:如图,在梯形ABCD中,AD∥BC,CA⊥AB,cos∠ABC=$\frac{\sqrt{5}}{5}$,BC=5,AD=2.求:(1)AC的长;
(2)∠ADB的正切值.
分析 (1)由三角函数求出AB,再由勾股定理求出AC即可;
(2)作AH⊥BC于H,交BD于E,得出∠HAC=∠ABC,由三角函数求出AH=$\frac{\sqrt{5}}{5}$AC=2,由勾股定理求出CH,得出BH,由平行线得证出△ADE∽△HBE,得出比例式求出AE,即可求出∠ADB的正切值.
解答 解:(1)∵CA⊥AB,cos∠ABC=$\frac{AB}{BC}$=$\frac{\sqrt{5}}{5}$,BC=5,
∴AB=$\sqrt{5}$,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$; (2)作AH⊥BC于H,交BD于E,如图所示:
(2)作AH⊥BC于H,交BD于E,如图所示:
∵CA⊥AB,
∴∠HAC=∠ABC,
∴cos∠HAC=$\frac{AH}{AC}$=cos∠ABC=$\frac{\sqrt{5}}{5}$,
∴AH=$\frac{\sqrt{5}}{5}$AC=2,
∴CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=,$\sqrt{20-4}$=4,
∴BH=BC-CH=5-4=1,
∵AD∥BC,
∴△ADE∽△HBE,
∴$\frac{AE}{EH}=\frac{AD}{BH}$=2,
∴AE=$\frac{2}{3}$AH=$\frac{4}{3}$,
∴tan∠ADB=$\frac{AE}{AD}$=$\frac{2}{3}$.
点评 本题考查了梯形的性质、解直角三角形、勾股定理、三角函数、相似三角形的判定与性质;熟练掌握解直角三角形,证明三角形相似是解决问题(2)的关键.

练习册系列答案
相关题目
14.直角三角形中,如果有两条边长分别为3,4,且第三条边长为整数,那么第三条边长应该是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
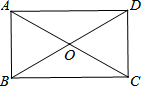 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=2,求AD的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AB=2,求AD的长.