题目内容
5.解下列方程.(1)$\frac{2x+1}{4}$-1=$\frac{10x+1}{12}$;
(2)2(2x-1)=2(1+x)+3(x+3);
(3)$\frac{0.1x-2}{0.3}$+$\frac{3-0.7x}{0.4}$=1;
(4)$\frac{4}{3}$[$\frac{6}{4}$($\frac{1}{5}$x-2)-6]=-2;
(5)$\left\{\begin{array}{l}{2a-3(a+2b)=1}\\{\frac{a+2b}{3}=1}\end{array}\right.$;
(6)$\left\{\begin{array}{l}{3x+2y=7}\\{6x-2y=11}\end{array}\right.$.
分析 (1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程整理后,去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去括号,移项合并,把x系数化为1,即可求出解;
(5)方程组整理后,利用加减消元法求出解即可;
(6)方程组利用加减消元法求出解即可.
解答 解:(1)去分母得:6x+3-12=10x+1,
移项合并得:4x=-10,
解得:x=-2.5;
(2)去括号得:4x-2=2+2x+3x+9,
移项合并得:x=-13;
(3)方程整理得:$\frac{x-20}{3}$+$\frac{30-7x}{4}$=1,
去分母得:4x-80+90-21x=12,
移项合并得:-17x=2,
解得:x=-$\frac{2}{17}$;
(4)去括号得:$\frac{2}{5}$x-4-8=-2,
移项合并得:$\frac{2}{5}$x=10,
解得:x=25;
(5)方程组整理得:$\left\{\begin{array}{l}{-a-6b=1①}\\{a+2b=3②}\end{array}\right.$,
①+②得:-4b=4,即b=-1,
把b=-1代入②得:a=5,
则方程组的解为$\left\{\begin{array}{l}{a=5}\\{b=-1}\end{array}\right.$;
(6)$\left\{\begin{array}{l}{3x+2y=7①}\\{6x-2y=11②}\end{array}\right.$,
①+②得:9x=18,即x=2,
把x=2代入①得:y=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 学习实践园地系列答案
学习实践园地系列答案| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
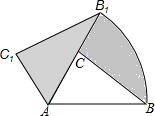 如图,在△ACB中,∠BAC=50°,AC=2,AB=3,现将△ACB绕点A逆时针旋转50°得到△AC1B1,则阴影部分的面积为$\frac{5}{4}$π.
如图,在△ACB中,∠BAC=50°,AC=2,AB=3,现将△ACB绕点A逆时针旋转50°得到△AC1B1,则阴影部分的面积为$\frac{5}{4}$π. 如图,在矩形ABCD中,点E、F分别在AB,CD边上,连接CE、AF,DF=BE,证明四边形AECF是平行四边形.
如图,在矩形ABCD中,点E、F分别在AB,CD边上,连接CE、AF,DF=BE,证明四边形AECF是平行四边形. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.