题目内容
7.三角形三条中位线的长分别为5、12、13,则此三角形的面积为( )| A. | 120 | B. | 240 | C. | 30 | D. | 60 |
分析 根据三角形的中位线定理即可求得△ABC的各个边长,利用勾股定理的逆定理可以判断△ABC是直角三角形,则面积即可求解.
解答 解:设中位线DE=5,DF=12,EF=13.
∵DE是△ABC的中位线,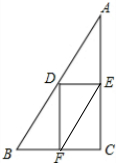
∴BC=2DE=2×3=10.
同理:AC=2DF=24,AB=2EF=26.
∵102+242=676=262,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×10×24=120.
故选:A.
点评 本题主要考查了勾股定理,以及三角形的中位线定理,正确求得△ABC的边长,判断△ABC是直角三角形是解题关键.

练习册系列答案
相关题目
19. 夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
(1)计算夏良该学期数学平时质量检测的平均成绩;
(2)如果学期总评成绩是按照图所示的权重计算,请计算出夏良该学期的数学总评成绩.
 夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):
夏良是一位有心的同学,他把自己八年级第一学期的数学质量检测成绩(单位:分)作了统计(如表):| 质量检测类型 | 平时 | 期中 | 期末 | |||
| 检测1 | 检测2 | 检测3 | 检测4 | |||
| 成绩 | 90 | 76 | 85 | 89 | 87 | 92 |
(2)如果学期总评成绩是按照图所示的权重计算,请计算出夏良该学期的数学总评成绩.
 如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.
如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH为a,BH为b,则ab=48.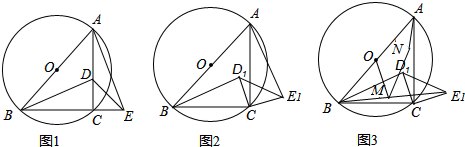
 如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12.
如图,在等腰△ABC中,AB=AC,点O是△ABC内一点,且OB=OC,联结AO并延长交边BC于点D,如果BD=6,那么BC的值为12.