题目内容
5. 在“爱满江阴”慈善一日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
在“爱满江阴”慈善一日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.(1)这50名同学捐款的众数为15元,中位数为15元.
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
分析 (1)根据众数的定义即出现次数最多的数据进而得出即可,再利用中位数的定义得出即可;
(2)利用条形统计图得出各组频数,再根据加权平均数的公式计算平均数,利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数.
解答 解:(1)数据15元出现了20次,出现次数最多,所以众数是15元;
数据总数为50,所以中位数是第25、26位数的平均数,即(15+15)÷2=15(元).
(2)(5×8+10×14+15×20+20×6+25×2)÷50=13(元);
估计这个中学的捐款总数=600×13=7800(元).
答:该校学生的捐款总数是7800元.
故答案为:15元,15元.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.除此之外,本题也考查了平均数、中位数、众数的定义以及利用样本估计总体的思想.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
10.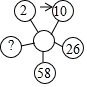 如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )
如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )
 如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )
如图,从左上角标注2的圆圈开始,顺时针方向按an+b的规律,(n表示前一个圆圈中的数字,a,b是常数)转换后得到下一个圆圈中的数,则标注“?”的圆圈中的数应是( )| A. | 119 | B. | 120 | C. | 121 | D. | 122 |
17.已知两个整数a,b,满足0<b<a<10,且$\frac{9a}{a+b}$是整数,那么数对(a,b)有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
 如图,⊙O中,若∠AOB的度数为56°,∠ACB=28°.
如图,⊙O中,若∠AOB的度数为56°,∠ACB=28°.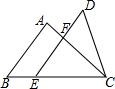 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )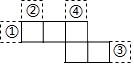 由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( )
由五个全等正方形组成的图形如图所示,将一个同样大小的正方形放在图中的①、②、③、④某一位置,所组成的图形不是正方体表面展开图的是( )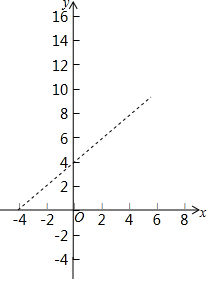 如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.
如图,已知 A(-4,0),B(0,4),现以A点为位似中心,相似比为4:9,将OB向右侧放大,B点的对应点为C.