Question

14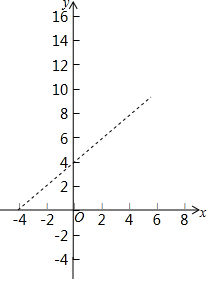．如图，已知 A（-4，0），B（0，4），现以A点为位似中心，相似比为4：9，将OB向右侧放大，B点的对应点为C．
（1）求C点坐标及直线BC的解析式；
（2）一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象；
（3）若点P是直线BC下方抛物线上的一点，求使△PBC面积为10时点P的坐标；
（4）现将直线BC绕B点旋转与抛物线相交于另一点Q，请找出抛物线上所有满足到直线AB距离为3$\sqrt{2}$的点Q．

Answer 1

分析 （1）利用相似及相似比，可得到C的坐标．把A，B代入一次函数解析式即可求得解析式的坐标．
（2）顶点落在x轴正半轴上说明此函数解析式与x轴有一个交点，那么△=0，再把B，C两点即可．
（3）如图由S_△OBC=$\frac{1}{2}$×4×5=10，过点O作BC的平行线交抛物线于P₁，P₂，此时△PBC的面积为10，构建方程组求交点坐标即可；
（4）到直线AB的距离为3 $\sqrt{2}$的直线有两条，可求出这两条直线解析式，和二次函数解析式组成方程组，求得点Q坐标．

解答 解：（1）过C点向x轴作垂线，垂足为D，由位似图形性质可知△ABO∽△ACD，
∴$\frac{AO}{AD}$=$\frac{BO}{CD}$=$\frac{4}{9}$．
由已知A（-4，0），B（0，4）可知
AO=4，BO=4．
∴AD=CD=9，
∴C点坐标为（5，9），
设直线BC的解析式为y=kx+b，
∵A（-4，0），B（0，4）在一次函数解析式上，那么
-4k+b=0，b=4，
解得k=1，
化简得y=x+4；

（2）设抛物线解析式为y=ax²+bx+c（a＞0），由题意得
$\left\{\begin{array}{l}{c=4}\\{25a+5b+c=9}\\{{b}^{2}-4ac=0}\end{array}\right.$，
解得 $\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=4}\end{array}\right.$，$\left\{\begin{array}{l}{a=\frac{1}{25}}\\{b=\frac{4}{5}}\\{c=4}\end{array}\right.$．，
∴解得抛物线解析式为y₁=x²-4x+4或y₂=$\frac{1}{25}$x²+$\frac{4}{5}$x+4，
又∵y₂=$\frac{1}{25}$x²+$\frac{4}{5}$x+4的顶点在x轴负半轴上，不合题意，故舍去．
∴满足条件的抛物线解析式为y=x²-4x+4，
函数y=x²-4x+4图象如图所示．

（3）如图∵S_△OBC=$\frac{1}{2}$×4×5=10，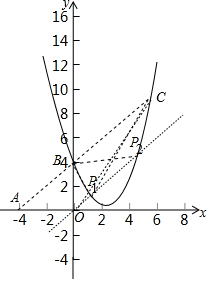

过点O作BC的平行线交抛物线于P₁，P₂，此时△PBC的面积为10．
由$\left\{\begin{array}{l}{y=x}\\{y={x}^{2}-4x+4}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$，
∴P₁（1，1），P₂（4，4）

（4）将直线BC绕B点旋转与抛物线相交于另一点P，设Q到直线AB的距离为h，
故Q点应在与直线AB平行，且相距3 $\sqrt{2}$的上下两条平行直线l₁和l₂上．
由平行线的性质可得
两条平行直线与y轴的交点到直线BC的距离也为3 $\sqrt{2}$，
如图，设l₁与y轴交于E点，过E作EF⊥BC于F点，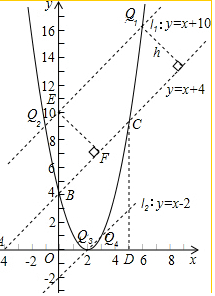

在Rt△BEF中EF=h=3 $\sqrt{2}$，∠EBF=∠ABO=45°，
∴BE=6．
∴可以求得直线l₁与y轴交点坐标为（0，10），
同理可求得直线l₂与y轴交点坐标为（0，-2），
∴两直线解析式l₁：y=x+10；l₂：y=x-2．
根据题意列出方程组：
（1）$\left\{\begin{array}{l}{y={x}^{2}-4x+4}\\{y=x+10}\end{array}\right.$；（2）$\left\{\begin{array}{l}{y={x}^{2}-4x+4}\\{y=x-2}\end{array}\right.$，
解得 $\left\{\begin{array}{l}{x=6}\\{y=16}\end{array}\right.$；$\left\{\begin{array}{l}{x=-1}\\{y=9}\end{array}\right.$；$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$； $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$，
∴满足条件的点P有四个，
它们分别是Q₁（6，16），Q₂（-1，9），Q₃（2，0），Q₄（3，1）．

点评 本题考查二次函数综合题、一次函数的应用、待定系数法、两直线平行的条件、二元二次方程组等知识，解题的关键是灵活运用所学知识解决问题，学会构建方程组解决交点问题，属于中考压轴题．