题目内容
13.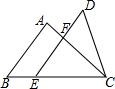 如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=6,EF=4,则DF的长是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 作CM⊥AB交EF于N,垂足为M.由EF∥AB,推出△CEF∽△CBA,推出$\frac{EF}{AB}$=$\frac{CN}{CM}$=$\frac{4}{6}$=$\frac{2}{3}$,设CN=2h,CM=3h,则MN=h,由S△ABC=S△CED,推出S四边形ABEF=S△DFC,列出方程即可解决问题.
解答 解:作CM⊥AB交EF于N,垂足为M.
∵EF∥AB,
∴△CEF∽△CBA,
∴$\frac{EF}{AB}$=$\frac{CN}{CM}$=$\frac{4}{6}$=$\frac{2}{3}$,设CN=2h,CM=3h,则MN=h,
∵S△ABC=S△CED,
∴S四边形ABEF=S△DFC,
∴$\frac{1}{2}$(AB+EF)•MN=$\frac{1}{2}$•DF•CN,
∴$\frac{1}{2}$(4+6)•h=$\frac{1}{2}$•DF•2h,
∴DF=5,
故选C.
点评 本题考查相似三角形的判定和性质、梯形的面积、三角形的面积等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
8.已知an=(-1)n+1,当n=1时,a1=0;当n=2时,a2=2;当n=3时,a3=0,…;则a1+a2+a3+…+a2017的值为( )
| A. | 1008 | B. | 1010 | C. | 2016 | D. | 2017 |
2. 小亮要判断△ABC的面积是△DBC的面积的几倍,现仅有一把有刻度的直尺,则至少需要测量的次数是( )
小亮要判断△ABC的面积是△DBC的面积的几倍,现仅有一把有刻度的直尺,则至少需要测量的次数是( )
 小亮要判断△ABC的面积是△DBC的面积的几倍,现仅有一把有刻度的直尺,则至少需要测量的次数是( )
小亮要判断△ABC的面积是△DBC的面积的几倍,现仅有一把有刻度的直尺,则至少需要测量的次数是( )| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(≈1.414 sin52°≈0.788,tan52°≈1.280)
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)(≈1.414 sin52°≈0.788,tan52°≈1.280)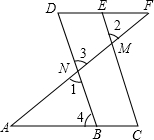 在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.
在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D. 在“爱满江阴”慈善一日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
在“爱满江阴”慈善一日捐活动中,某学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.