题目内容
3.4张相同的卡片上分别写有数字2,3,4,5将卡片的背面向上,洗匀后从中任意抽取1 张,将卡片上的数字作为被减数;一只不透明的袋子中装有标号2,3,4的3个小球,这些球除标号外都相同,搅匀后从中任意摸出一个球,将摸到的球的标号作为减数.(1)用树状图或列表的方法求这两个数的差为0的概率;
(2)如果游戏规则规定:当抽到的这两个数的差为非负数时,则甲获胜;否则,乙获胜,
你认为这样的规则公平吗?如果不公平,请说明理由.
分析 (1)利用树状图法列举出所有可能,进而求出概率;
(2)利用概率公式进而得出甲、乙获胜的概率即可得出答案.
解答 解:(1)画树状图如下:
由树状图可知,共有12种等可能结果,其中差为0的有3种结果,
∴这两个数的差为0的概率为$\frac{3}{12}$=$\frac{1}{4}$;
(2)由(1)中树状图可知,两个数的差为非负数的有9种结果,
∴甲获胜的概率为$\frac{9}{12}$=$\frac{3}{4}$,
则乙获胜的概率为1-$\frac{3}{4}$=$\frac{1}{4}$,
∴此游戏不公平.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个参与者取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
13.已知实数x、y、z满足:(x+z)2-4(x-y)(y+z)=0,下列式子一定成立的是( )
| A. | x+y-z=0 | B. | x+y+2z=0 | C. | y-z-2x=0 | D. | -z+x-2y=0 |
14.传统佳节“春节”临近,剪纸民俗魅力四射,对称现象无处不在.观察下面的四幅剪纸,其中是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.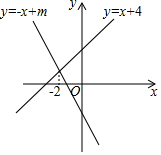 如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )
如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )
 如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )
如图,直线y=-x+m与y=x+4的交点的横坐标为-2,则关于x的不等式-x+m>x+4的解集为( )| A. | x>-2 | B. | x<-2 | C. | x>-4 | D. | x<-4 |
13.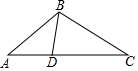 如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )
如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )
 如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )
如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AD}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{BD}{BC}$ |
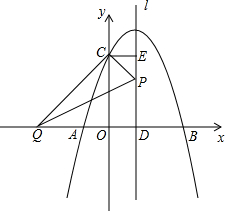 如图,二次函数y=ax2+bx+c的图象与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
如图,二次函数y=ax2+bx+c的图象与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).