题目内容
8．以点A（-4，1），B（-4，-3）为端点的线段AB上的任意一点的坐标可表示（-4，y）（-3≤y≤1）．分析 由两点的坐标可知两点在直线x=-4上，然后再写出满足题目的条件的x的取值范围即可．
解答 解：∵A（-4，1），B（-4，-3）为端点的线段在直线x=4上，
∴在两点为端点的线段上任意一点可表示为：（-4，y）（-3≤y≤1），
故答案为：（-4，y）（-3≤y≤1）．
点评 本题主要考查坐标与图形性质，此题涉及到函数思想，注意线段上的点包括两端点是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
19．下列分式的变形正确的是（ ）
| A． | $\frac{a}{a-1}-\frac{1}{a-1}=1$ | B． | $\frac{m}{{{m^2}+1}}=\frac{1}{m+1}$ | C． | $\frac{{{x^2}-1}}{x-1}=x-1$ | D． | $\frac{-a-1}{a+1}=-\frac{a-1}{a+1}$ |
16．
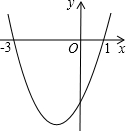如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3，1，则下列结论正确的个数有（ ）
①ac＞0；②2a-b=0；③4a-2b+c＞0；④对于任意实数m均有am2+bm≥a-b．
如图，二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3，1，则下列结论正确的个数有（ ）①ac＞0；②2a-b=0；③4a-2b+c＞0；④对于任意实数m均有am2+bm≥a-b．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
20．下列运用等式性质正确的是（ ）
| A． | 如果a=b，那么a+c=b-c | B． | 如果a=b，那么$\frac{a}{c}=\frac{b}{c}$ | ||
| C． | 如果$\frac{a}{c}=\frac{b}{c}$，那么a=b | D． | 如果a=3，那么a2=3a2 |
18．下列说法错误的是（ ）
| A． | 数字0也是单项式 | B． | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ | ||
| C． | 1-a-ab是二次三项式 | D． | 多项式2x2+3x-5中，常数项为5 |