题目内容
11.反比例函数y=$\frac{k+1}{x}$的图象经过A(x1,y1),B(x2,y2)两点,其中x1<0<x2且y1>y2,则k的范围是k<-1.分析 根据给出的条件确定双曲线所在的象限,然后列出不等式解出k的范围.
解答 解:∵x1<0<x2时,y1>y2,
∴双曲线在第二,四象限,
∴k+1<0,
解得k<-1,
故答案为:k<-1.
点评 本题考查的是反比例函数图象的性质、反比例函数图象上点的坐标特征,掌握反比例函数的性质与k的关系是解题的关键.

练习册系列答案
相关题目
1.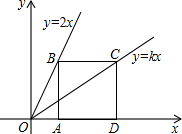 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
 如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )
如图,点B、C分别在直线y=2x和y=kx上,点A,D是x轴上的两点,已知四边形ABCD是正方形,则k的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
19.下列分式的变形正确的是( )
| A. | $\frac{a}{a-1}-\frac{1}{a-1}=1$ | B. | $\frac{m}{{{m^2}+1}}=\frac{1}{m+1}$ | C. | $\frac{{{x^2}-1}}{x-1}=x-1$ | D. | $\frac{-a-1}{a+1}=-\frac{a-1}{a+1}$ |
16.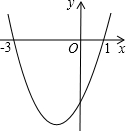 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
①ac>0;②2a-b=0;③4a-2b+c>0;④对于任意实数m均有am2+bm≥a-b.
 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-3,1,则下列结论正确的个数有( )①ac>0;②2a-b=0;③4a-2b+c>0;④对于任意实数m均有am2+bm≥a-b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.下列运用等式性质正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | ||
| C. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | D. | 如果a=3,那么a2=3a2 |
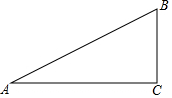 如图,Rt△ABC中,∠C=90°,∠A=30°.
如图,Rt△ABC中,∠C=90°,∠A=30°.