题目内容
13.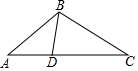 如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )
如图,△ABC中,点D在AC边上,添加下列条件后仍不能判别△ABD∽△ACB的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AD}{AB}$=$\frac{AB}{AC}$ | D. | $\frac{AD}{AB}$=$\frac{BD}{BC}$ |
分析 由图可知△ABC与△ABD中∠A为公共角,所以只要再找一组角相等,或一组对应边成比例即可满足△ABD∽△ACB;得出选项A、B、C满足△ABD∽△ACB,选项D不满足△ABD∽△ACB,即可得出结论.
解答 解:∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴选项A不符合;
∵∠ADB=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴选项B不符合;
∵$\frac{AD}{AB}$=$\frac{AB}{AC}$,∠A=∠A,
∴△ABD∽△ACB,
∴选项C不符合;
虽然$\frac{AD}{AB}$=$\frac{BD}{BC}$,但∠A≠∠B,
∴△ABD与△ACB不相似,
∴选项D符合.
故选:D.
点评 本题考查了相似三角形的判定,此题主要考查学生对相似三角形判定定理的理解和掌握,难度不大,属于基础题,要求学生应熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.化简(1+$\frac{{a}^{2}}{1+2a}$)÷$\frac{1+a}{1+2a}$的结果为( )
| A. | $\frac{1}{1+2a}$ | B. | 1+a | C. | $\frac{1}{1+a}$ | D. | 1-a |
18.下列说法错误的是( )
| A. | 数字0也是单项式 | B. | -$\frac{2ab}{3}$的系数是-$\frac{2}{3}$ | ||
| C. | 1-a-ab是二次三项式 | D. | 多项式2x2+3x-5中,常数项为5 |
3.若函数y=2x2-8x+m的图象上有两点A(x1,y1),B(x2,y2),若x1<x2<-2,则( )
| A. | y1<y2 | B. | y1>y2 | ||
| C. | y1=y2 | D. | y1、y2、的大小不确定 |
 如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是ab-$\frac{π{b}^{2}}{4}$.
如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是ab-$\frac{π{b}^{2}}{4}$.