题目内容
5. 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.(1)求证:AB=AC;
(2)若AB=10,BC=12,求cos∠ABD的值.
分析 (1)先连结AE,根据ASA判定△AEB≌△AEC,再根据全等三角形的性质得出AB=AC;
(2)先根据等腰三角形的性质以及勾股定理,求得AE和BE的长,再根据面积法求得BD的长,最后计算cos∠ABD的值.
解答 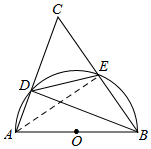 (1)方法一:连结AE,
(1)方法一:连结AE,
∵AB是直径,
∴∠AEB=∠AEC=90°,
∵$\widehat{DE}=\widehat{BE}$,
∴∠BAE=∠CAE,
又AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC;
方法二:∵AB是直径,
∴∠ADB=∠CDB=90°,
∵$\widehat{DE}=\widehat{BE}$,
∴DE=BE,
∴∠CBD=∠BDE,
∴∠C=∠CDE,
∵ABED是圆内接四边形,
∴∠CDE=∠CBA,
∴∠C=∠CBA,
∴AB=AC;
(2)由(1)知△ABC为等腰三角形,AE⊥BC,
∴BE=CE=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6,
∵在Rt△ABE中,AB=10,BE=6,
∴AE=$\sqrt{{{10}^2}-{6^2}}$=8,
∵AB是直径,
∴∠ADB=90°,
∴$\frac{1}{2}AE•BC=\frac{1}{2}BD•AC$,
∴$BD=\frac{8×12}{10}=\frac{48}{5}$,
∴$cos∠ABD=\frac{BD}{AB}=\frac{{\frac{48}{5}}}{10}=\frac{24}{25}$.
点评 本题主要考查了全等三角形的判定与性质、圆周角定理以及勾股定理的综合应用,解决问题的关键是作辅助线,构造全等三角形.解题时注意面积法的运用.

练习册系列答案
相关题目
14.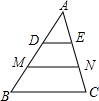 如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
 如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )
如图,在△ABC中,D、M在AB上,E、N在AC上且AD=DM=MB,AE=EN=NC,△ADE、梯形DMNE、梯形MBCN的面积比为( )| A. | 1:2:3 | B. | 1:4:9 | C. | 1:3:5 | D. | 1:3:7 |
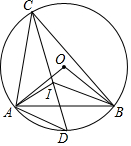 如图,△ABC的外接圆为⊙O,I为△ABC的内心,∠ACB=50°,CI的延长线交⊙O于点D.
如图,△ABC的外接圆为⊙O,I为△ABC的内心,∠ACB=50°,CI的延长线交⊙O于点D. 如图,在△ABC中,已知∠B=30°,∠C=45°,AB=6,AC=3$\sqrt{2}$,求BC的长.
如图,在△ABC中,已知∠B=30°,∠C=45°,AB=6,AC=3$\sqrt{2}$,求BC的长.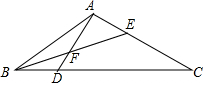 如图,D是△ABC的边BC上的点,∠BAD=∠C,BE是△ABC的角平分线,交AD于点F,BD=2,CD=5,则BE:BF=$\sqrt{14}$:2.
如图,D是△ABC的边BC上的点,∠BAD=∠C,BE是△ABC的角平分线,交AD于点F,BD=2,CD=5,则BE:BF=$\sqrt{14}$:2.