题目内容
15.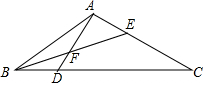 如图,D是△ABC的边BC上的点,∠BAD=∠C,BE是△ABC的角平分线,交AD于点F,BD=2,CD=5,则BE:BF=$\sqrt{14}$:2.
如图,D是△ABC的边BC上的点,∠BAD=∠C,BE是△ABC的角平分线,交AD于点F,BD=2,CD=5,则BE:BF=$\sqrt{14}$:2.
分析 首先证明△ABD∽△CBA,得$\frac{AB}{BC}$=$\frac{BD}{AB}$,求出AB,再证明△CBE∽△ABF,得$\frac{BE}{BF}$=$\frac{BC}{AB}$,由此即可解决问题.
∴$\frac{BE}{BF}$=$\frac{BC}{AB}$=
解答  解:∵∠ABD=∠CBA,∠BAD=∠C,
解:∵∠ABD=∠CBA,∠BAD=∠C,
∴△ABD∽△CBA,
∴$\frac{AB}{BC}$=$\frac{BD}{AB}$,
∴$\frac{AB}{7}$=$\frac{2}{AB}$,
∴AB2=14,
∵AB>0,
∴AB=$\sqrt{14}$,
∵∠ABF=∠EBC,∠BAF=∠C,
∴△CBE∽△ABF,
∴$\frac{BE}{BF}$=$\frac{BC}{AB}$=$\frac{7}{\sqrt{14}}$=$\frac{\sqrt{14}}{2}$.
故答案为$\sqrt{14}$:2.
点评 本题考查相似三角形的判定和性质.解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
6.已知x2=4,|y|=9,且xy<0,则x+y的值等于( )
| A. | ±7 | B. | ±11 | C. | -7或11 | D. | -7或-11 |
 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.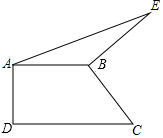 如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得到线段BE,连接AE.若AB=2,DC=4,则△ABE的面积为2.
如图,在四边形ABCD中,AB⊥AD,CD⊥AD,将BC按逆时针方向绕点B旋转90°,得到线段BE,连接AE.若AB=2,DC=4,则△ABE的面积为2.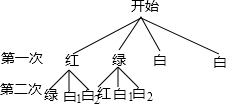 一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.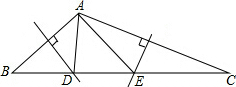 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=10,则△ADE周长是多少?为什么?
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.若BC=10,则△ADE周长是多少?为什么?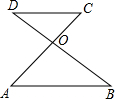 如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.
如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.