题目内容
17.在△ABC中,已知BC=$\sqrt{6}$,∠A=60°,∠C=45°,那么AC的长为1+$\sqrt{3}$.分析 过B点作BD⊥AC于D,如图,先利用△BDC为等腰直角三角形得到CD=BD=$\frac{\sqrt{2}}{2}$BC=$\sqrt{3}$,然后在Rt△ABD中,利用tanA可计算出AD,然后计算AD+CD即可.
解答 解:过B点作BD⊥AC于D,如图,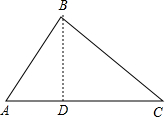
在Rt△BDC中,∵∠C=45°,
∴△BDC为等腰直角三角形,
∴CD=BD=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$×$\sqrt{6}$=$\sqrt{3}$,
在Rt△ABD中,∵tanA=$\frac{BD}{AD}$,
∴AD=$\frac{\sqrt{3}}{\sqrt{3}}$=1,
∴AC=AD+CD=1+$\sqrt{3}$.
故答案为1+$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.熟练掌握勾股定理和三角函数的定义是解决此类问题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.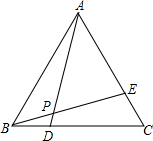 如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
 如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )
如图,在等边△ABC中,D、E分别是BC、AC上的点,且BD=CE,AD与BE相交于点P.下列结论:①AE=CD;②AD=BE;③∠AEB=∠ADC;④∠APE=60°.其中正确的结论共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.已知x2=4,|y|=9,且xy<0,则x+y的值等于( )
| A. | ±7 | B. | ±11 | C. | -7或11 | D. | -7或-11 |
 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.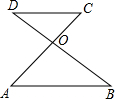 如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.
如图,已知AC和BD交于点O,AB∥CD,OA=OB,求证:OC=OD.