题目内容
4.(1)计算:(-2015)0×|-3|-32+$\sqrt{8}$;(2)解方程:$\frac{1}{x-1}$-$\frac{3}{1-x}$=2.
分析 (1)原式利用零指数幂法则,绝对值的代数意义,乘方的意义,以及二次根式的性质计算即可得到结果;
(2)分式方程变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=1×3-9+2$\sqrt{2}$=-6+2$\sqrt{2}$;
(2)去分母得:1+3=2(x-1),
解得:x=3,
经检验x=3是分式方程的解.
点评 此题考查了实数的运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.使$\frac{\sqrt{x-3}}{x-4}$有意义的x的取值范围是( )
| A. | x≥3 | B. | x≥3且x≠4 | C. | x≤3 | D. | x<3 |
15.下列各式成立的是( )
| A. | 4<$\sqrt{11}$<5 | B. | (x+1)(x+2)=x2+3x+2 | C. | 2-3=3-2 | D. | x3•x2=x3-x2 |
19.抛物线y=-(x-2)2-3的顶点坐标是( )
| A. | (-2,-3) | B. | (2,3) | C. | (-2,3) | D. | (2,-3) |
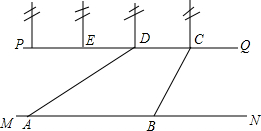 如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)
如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m) 如图,已知等边△ABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
如图,已知等边△ABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.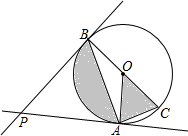 如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠P=60°,若BC为⊙O的直径,则图中阴影部分的面积为π.
如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠P=60°,若BC为⊙O的直径,则图中阴影部分的面积为π.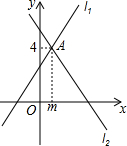 如图,直线l1:y=x+3与直线l2:y=ax+b相交于点A(m,4).
如图,直线l1:y=x+3与直线l2:y=ax+b相交于点A(m,4).