题目内容
12.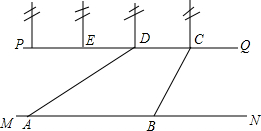 如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)
如图,河流的两岸MN,PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C,D,E…某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了120m到达B处,测得∠CBN=60°.求河流的宽度.(结果精确到0.1m)
分析 作DK∥CB,交MN于K,作DH⊥MN,垂足为H.判断出四边形DCBK为平行四边形,再判断出DH=xtan60°=$\sqrt{3}$x米,在Rt△AHD中,得到$\frac{\sqrt{3}x}{x+70}$=tan30°,求出x即可.
解答 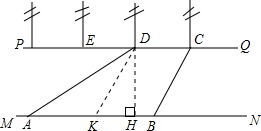 解:作DK∥CB,交MN于K,作DH⊥MN,垂足为H.
解:作DK∥CB,交MN于K,作DH⊥MN,垂足为H.
∵CD∥KB,BC∥KB,
∴四边形DCBK为平行四边形,
∴KB=DC=50米,
∴AK=(120-50)=70米,
设KH=x米,
则DH=xtan60°=$\sqrt{3}$x米,
在Rt△AHD中,$\frac{\sqrt{3}x}{x+70}$=tan30°,
∴$\frac{\sqrt{3}x}{x+70}$=$\frac{\sqrt{3}}{3}$,
∴x=35,
DH=35$\sqrt{3}$≈60.6米.
答:河流宽约为60.6米.
点评 本题考查了解直角三角形的应用,构造合适的直角三角形是集体的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.矩形的对角线所成的角之一是65°,则对角线与各边所成的角度是( )
| A. | 57.5° | B. | 32.5° | C. | 57.5°,23.5° | D. | 57.5°,32.5° |
17.若非零实数x,y满足4y=3x,则x:y等于( )
| A. | 3:4 | B. | 4:3 | C. | 2:3 | D. | 3:2 |
1.在一次体育测试中,小芳所在小组8人的成绩分别是66,67,78,78,79,79,79,80,则这8人体育成绩的中位数是( )
| A. | 77 | B. | 78 | C. | 78.5 | D. | 79 |
 已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.
已知:当x>0时,反比例函数y1=$\frac{4}{x}$和y2=-$\frac{5}{x}$的图象在坐标系中的位置如图所示,直线y3=-x+b与两图象分别交于点A,B.