题目内容
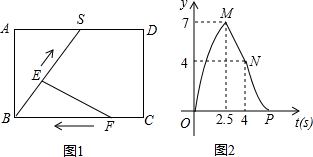
7. 已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P.
已知,如图1在Rt△ABC中,∠A=90°,AC=AB=2$\sqrt{2}$,D、E分别是AB、AC的中点,若等腰Rt△ABC绕点A逆时针旋转,得到等腰Rt△AB1C1,设旋转角α(0<α<360°),记直线DB1与EC1的交点为P.(1)如图2,当α=135°时,直线DB1与EC1的位置关系是DB1⊥EC1
(2)如图3,当α=90°时,求点P到直线AD的距离;
(3)当△ABC绕点A逆时针旋转一周时,点P到直线AD的距离是否存在最大值?若存在,求出P点到直线AD的最大距离;若不存在,请说明理由.
分析 (1)利用旋转的性质可知:∠B1AD=C1AE,根据题意可证明△B1AD≌△C1AE,所以∠AB1D=∠AC1E,从而可知∠B1PC1=∠B1AC1=90°,所以DB1⊥EC1;
(2)过点P作PF⊥AD于点F,可知△B1AD≌△C1AE,从而∠B1PC1=∠B1AC1=90°,所以易证△B1PE∽△C1AE,利用相似三角形的性质即可求出PE的长度,再证明△C1AE∽△C1FP,利用相似三角形的性质即可求出PF的长度;
(3)在旋转的过程中,∠EPD始终保持为90°,点P在以ED为直径的圆上,又因为∠EAD=90°,点P在△EAD的外接圆上,即当PF过ED的中点时,点P到直线AD的距离最大.
解答 解:(1)当α=135°时,
由旋转的性质可知:∠B1AD=C1AE=135°,
∵△ADE与△ABC是等腰直角三角形,
∴AB1=AC1,AD=AE,
在△B1AD与△C1AE中,
$\left\{\begin{array}{l}{A{B}_{1}=A{C}_{1}}\\{∠{B}_{1}AD=∠{C}_{1}AE}\\{AD=AE}\end{array}\right.$,
∴△B1AD≌△C1AE(SAS),
∴∠AB1D=∠AC1E,
∴∠B1PC1=∠B1AC1=90°,
∴DB1⊥EC1,
故答案为:DB1⊥EC1;
(2) 过点P作PF⊥AD于点F,
过点P作PF⊥AD于点F,
由(1)可知:∴△B1AD≌△C1AE(SAS),
∴∠AB1D=∠AC1E,
∴∠B1PC1=∠B1AC1=90°,
∴△B1PE∽△C1AE,
∴$\frac{{C}_{1}E}{{B}_{1}E}=\frac{AE}{PE}$,
∵点E是AC的中点,
∴AE=B1E=$\frac{1}{2}$AC1=$\sqrt{2}$,
∴由勾股定理可求得:C1E=$\sqrt{10}$,
∴$\frac{\sqrt{10}}{\sqrt{2}}=\frac{\sqrt{2}}{PE}$,
∴PE=$\frac{\sqrt{10}}{5}$,
∴C1P=C1E+PE=$\frac{6}{5}\sqrt{10}$,
∵PF∥AE,
∴△C1AE∽△C1FP,
∴$\frac{{C}_{1}E}{{C}_{1}P}=\frac{AE}{PF}$,
∴$\frac{\sqrt{10}}{\frac{6}{5}\sqrt{10}}=\frac{\sqrt{2}}{PF}$,
∴PF=$\frac{6}{5}\sqrt{2}$;
(3)当△ABC绕点A逆时针旋转一周时
由旋转的性质可知:∠B1AD=C1AE,
∴△B1AD≌△C1AE,
∴∠AB1D=∠AC1E,
∴∠B1PC1=∠B1AC1=90°,
∴∠EPD=90°,
∴点P在以ED为直径的圆上,
∵∠EAD=90°,
∴点P在△EAD的外接圆上,如图4,
∴当PF过ED的中点时,点P到直线AD的距离最大,
设ED的中点为O,
∵∠EDA=45°,
∴OF=FD=$\frac{1}{2}$AD=$\frac{\sqrt{2}}{2}$,
∵AD=AE=$\sqrt{2}$,
∴由勾股定理可求得:ED=2,
∴OP=$\frac{1}{2}ED$=1,
∴PF=OP+OF=1+$\frac{\sqrt{2}}{2}$,
∴P点到直线AD的最大距离为1+$\frac{\sqrt{2}}{2}$.
点评 本题考查旋转的综合问题,涉及旋转的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,考查学生综合运用知识的能力.

 如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )
如图,在△ABC中,BC=6,∠A=90°,∠B=70°.把△ABC沿BC方向平移到△DEF的位置,若CF=2,则下列结论中错误的是( )| A. | BE=2 | B. | ∠F=20° | C. | AB∥DE | D. | DF=6 |
| A. | 2a(3a-1)=6a3-1 | B. | x•x3=x3 | C. | (-2xy2)4=16x4y8 | D. | x3+x3=x6 |
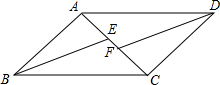 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.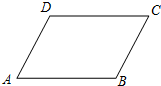 如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件:
如图,已知四边形ABCD中,AB∥CD,若不添加任何辅助线,请添加一个条件: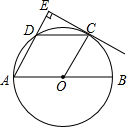 如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E
如图所示,AB是⊙O的直径,点C是$\widehat{BD}$的中点,∠COB=60°,过点C作CE⊥AD,交AD的延长线于点E 在?ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
在?ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.